A man pulls a solid cylinder $($ initially at rest $)$ horizontal by a massless string. The string is wrapped on the cylinder and the cylinder performs pure rolling. Mass of the cylinder is $100 k g$ , radius is $π$ metre $&$ tension in string is $100 N$ . Then the angular speed of the cylinder after one revolution will be $:$

A

$4 r a d / sec$

B

$\frac{4}{\sqrt{3}} r a d / sec$

C

$\frac{4}{3} r a d / sec$

D

non of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

The cylinder rolls without slipping, hence no work is being doen by friction. In one complete revolution the centre $C$ of the cylinder moves by $2 π R (R$ is radius of cylinder $)$ and the top most point $P$ of the cylinder moves by $4 π R$ .

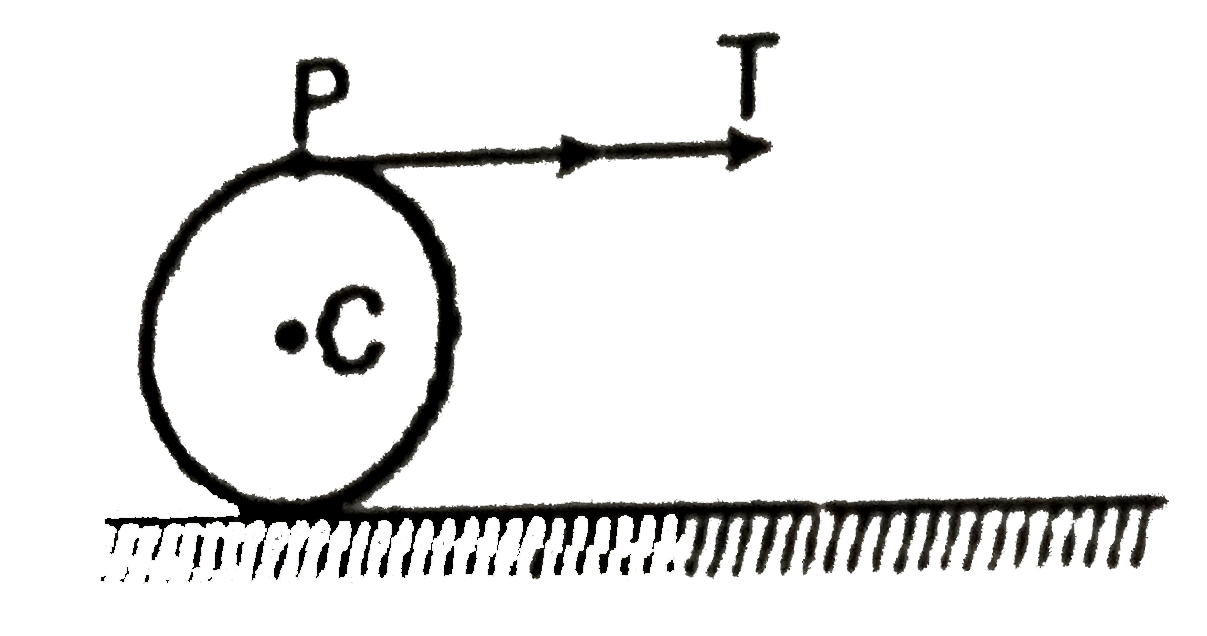
$v_{c m} = R ω ($ from constraint $)$
Applying work energy theorem
Work done by $T =$ increase in kinetic energy of cylinder
$T \times 4 π R = \frac{1}{2} I_{c m} ω^{2} + \frac{1}{2} m v_{c m}^{2} = \frac{1}{2} (\frac{1}{2} m R^{2}) ω^{2} + \frac{1}{2} m R^{2} ω^{2}$
solving we get $ω = \frac{4}{\sqrt{3}} r a d / sec$

|

Updated on:21/07/2023

Class 11 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A string is wrapped around a cylinder of mass $M$ and radius $R$ . The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
A $2 M g / 3$
B $M g / 2$
C $M g / 3$
D $M g / 6$
Question 2 - Select One
A string is wrapped around a cylinder of mass $M$ and radius $R$ . The string is pulled vertically upwards to prevent the centre of mass from falling as the cylinder unwinds the string. The tension in the string is
A $\frac{M g}{6}$
B $\frac{M g}{3}$
C $\frac{M g}{2}$
D $\frac{2 M g}{3}$
Question 3 - Select One
A solid cylinder of mass $50 k g$ and radius $0.5 m$ is free to rotate about the horizontal axis. A massless string is wound round the cylinder with one end attached to it and other end hanging freely. Tension in the string required to produce an angular acceleration of $2$ revolution $s^{- 2}$ is
A $25 N$
B $50 N$
C $78.5 N$
D $157 N$

RESONANCE-DAILY PRACTICE PROBLEMS-dpp 68

Home
Ask Doubt
Profile