One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O. The ball is released from a rest at t=0 with string horizontal and just taut. The ball then moves invertical circular path as shown. The time taken by ball to go from position A to B is t1 and from B to lowest position B to lowest position C is t2. Let the velocity of ball at B is →vB and C is →vC respectively.

If |→vC|=|→vB| then the value of θ as shown is
cos−1(1)4
sin−1(1)4
cos−1(1)2
sin−1(1)2
The correct Answer is:B
VB=√2gLsinθ and VC=√2gL
VC=2VB
Then 2gL=4(2gLsinθ)
or sinθ=14 or θ=sin−1(14)
Similar Questions
One end of a light string of length L is connected to a ball and the other end is connected to a fixed point O . The ball is released from a rest at t=0 with string horizontal and just taut. The ball then moves invertical circular path as shown. The time taken by ball to go from position A to B is t_(1) and from B to lowest position B to lowest position C is t_(2) . Let the velocity of ball at B is vec(v)_(B) and C is vec(v)_(C) respectively. If |vec(v)_(C)-vec(v)_(B)|=|vec(v)_(B)| , then the value of theta as shown is :
10:11View SolutionTwo balls having masses m and 2m are fasrtened to two light strings of same length (figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. Point A is the lowest point at which either ball can reach
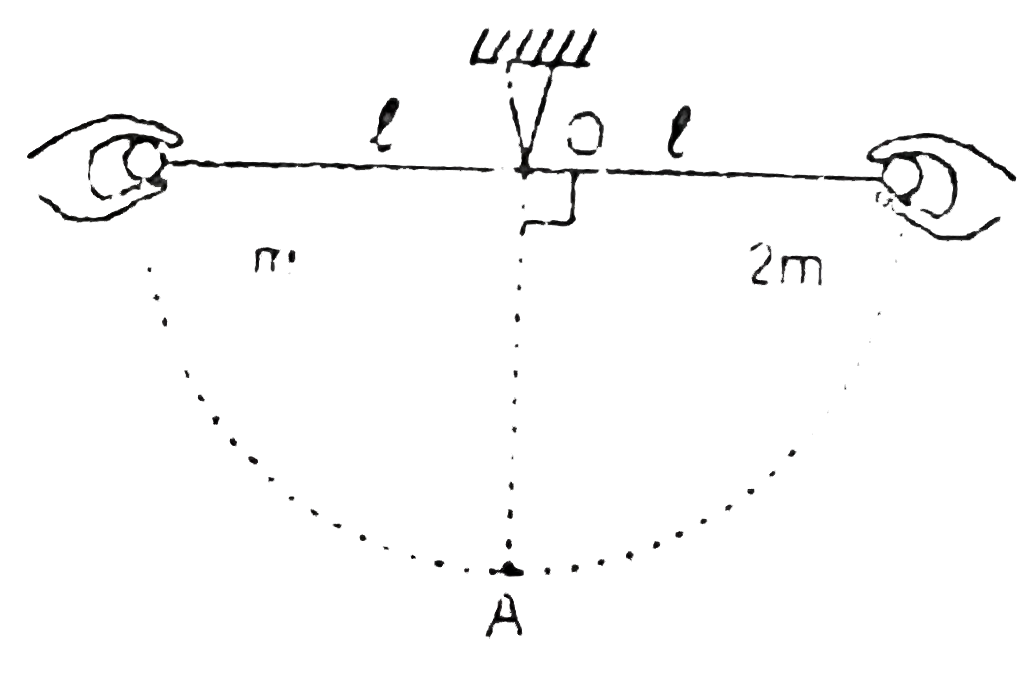
The position at which the balls will collide for the first time02:19View SolutionOne end of a light of length L is connected to a ball and other end is connected to a fixed point O . The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves it vertival circular pathh as shown. The time taken by ball to go from position A to B is t_(1) and from B to lowest position C is t_(2) . Let the velocity of ball at B is vecv_(B) and at C is vecv_(C) respectively. if |vecv_(c)|=2|vecv_(B)| then the value of theta shown is
05:23View SolutionOne end of a light of length L is connected to a ball and other end is connected to a fixed point O. The ball is released from rest at t=0 with string horizontal and just taut. The ball then moves it vertival circular pathh as shown. The time taken by ball to go from position A to B ist1 and from B to lowest position C is t2. Let the velocity of ball at B is →vB and at C is →vC respectively.

If |→vc|=2|→vB| then07:46View SolutionA pendulum is made by attaching a ball at the end of a string (the other end of the string is attached to the ceiling). The ball is released from rest at the position shown at some angle ϕ. Which of the following vectors may represent the impulse delivered by the string to the ball from the time it is released unitl the ball is at the bottom of the swing when string becomes vertical
 View Solution
View SolutionA small ball is suspended from a fixed point 'O' by means of a light and inextensible string of length 'l'. The ball is first taken aside such that string becomes horizontal and then released from rest. At the borrom it collides with a fixed obstacle. The co-efficient of restitution is 'e'. Find the maximum angular deflection of the string after n^(th) collision.
04:58View SolutionA ball is connected to an ideal string of length l=1.0 m whose other endis fixed to the point A. ball is released from the point B such that it can move in the vertical plane. Height of the point A above the ground is more than the length of string.The velocity of the ball at the lowest point of its motion is
 View Solution
View SolutionA ball of mass 1kg is attached to an inextensible string. The ball is released from the position shown in figure. Find the impulse imparted by the string to the ball immediately after the string becomes taut. (Take g=10m//s^2 )
02:45View Solution

