A solid ball of mass 'm' is released on a rough fixed inclined plane from height H. The ball will perform pure rolling on the inclined plane. Then
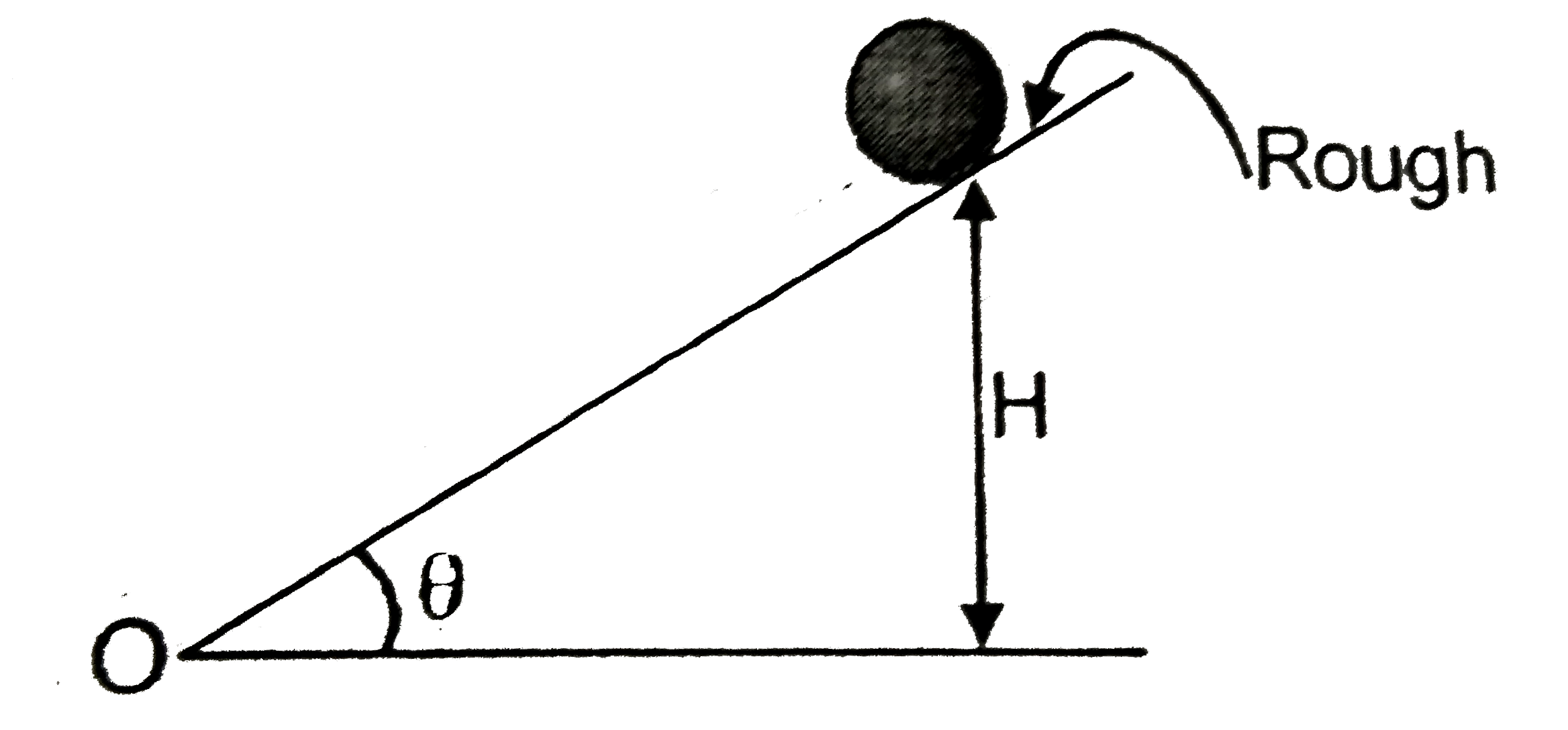
Kinetic energy of the ball at O will be less than mgH
Translational kinetic energy of the ball at O will be 5mgH7
Rotational kinetic energy of the ball atO will be 2mgH7
Angular momentum of the ball will be conserved about a point on the inclined plane.
The correct Answer is:B, C, D
In pure rolling static friction acts so energy remains conserved . So kinetic energy of ball at O=mgh
mgh=12mv2+12×25mr2v2r2
translational Rotational
kinetic energy kinetic
mgh=12mv2+15mv2
Translational kinetic energy=mgh×1212+12
=mgh×12710=5mgh7
Rotational kinetic enrgy =2mgh7
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 755videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 765videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp734videos
DAILY PRACTICE PROBLEMS
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise54videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems9videos
ELASTICITY AND VISCOCITY
Similar Questions
Knowledge Check
- Question 1 - Select One
A solid cylinder and a solid sphere, both having the same mass and radius, are released from a rough inclined plane of inclination θ one by one. They roll on the inclined plane without slipping. The force of friction that acts
Aon the two bodies is the sameBon the sphere is less than that for a cylinderCon the sphere is more than that for a cylinderDon the two bodies is independent of their sizes and shapes - Question 2 - Select One
A uniform solid spherical ball is rolling down a smooth inclined plane from a height h. The velocity attained by the ball when it reaches the bottom of the inclined plane is v. If the ball is now thrown vertically upwards with the same velocity v, the maximum height to which the ball will rise is
A5h/8B3h/5C5h/7D7h/9 - Question 3 - Select One
A uniform solid spherical ball is rolling down a smooth inclined plane from a height h. The velocity attained by the ball when it reaches the bottom of the inclined plane is v. If the ball is now thrown vertically upwards with the same velocity v, the maximum height to which the ball will rise is
A5h/8B3h/5C5h/7D7h/9
A solid cylinder of mass m is resting on fixed rough inclined plane with help of a thread. Find friction force between cylinder and inclined plane. (given μ=0.4)
 View Solution
View SolutionA solid cylinder is rolling down a rough inclined plane of inclination θ. Then
View SolutionA block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
View SolutionA uniform solid spherical ball is rolling down a smooth inclined plane from a height h. The velocity attained by the ball when it reaches the bottom of the inclined plane is v. If ball when it reaches the bottom of the inclined plane is v. If the ball is now thrown vertically upwards with the same velocity v, the maximum height to which the ball will rise is
View SolutionA uniform solid spherical ball is rolling down a smooth inclined plane from a height h. The velocity attained by the ball when it reaches the bottom of the inclined plane is v. If ball when it reaches the bottom of the inclined plane is v. If the ball is now thrown vertically upwards with the same velocity v, the maximum height to which the ball will rise is
View Solution

