A sinusoidal wave propagates along a string. In figure (a) and (b)'y' represents displacement of aprticle from the mean position. 'x'&'t' have usual meanings . Find :
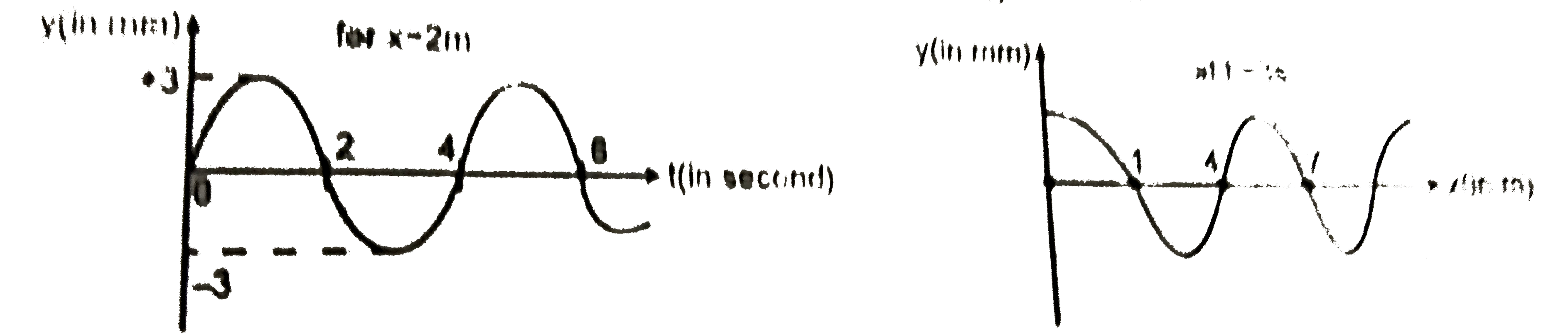
(a) wavelength, freuency and speed of the wave.
(b) maximum velocity and maximum acceleration of the particles.
(c) the magnitude of slopes of the string at x=2 at t=4sec.
The correct Answer is:(a) 6m,0.25Hz,1.5m//s
(b) 1.5pi mm//s, 0.75pi^(2) mm//s© pi
(a) from y−x graph
wavelength =λ=6m
from y−t graph
Time period =T=4sec
⇒frequency =f=14=0.25Hz
wave speed =fλ=0.25×6=1.50m/s
(b) maximum =3mm×π2rad/sec=1.5πmm/sec
maximum acceleration =w2A=π24×3mm=0.75p2mm/sec2.
(c)k=2πλ=π3m−1
⇒w=2πT=π2rad/sec
y=3sin(π3×−π2t+θ0)
y(x=2,t=0)=0
⇒sin(2π3+θ0)=0
⇒θ0=−2π3 or π3
and ∂y∂t(t=0,x=2)>0
⇒−3π2cos(π3x−πt2+θ0)>0
( For x=2,t=0)
⇒cos(2π3+θ0)<0
⇒θ0=π3
y=(x,t)=3sin(πx3−πt2+π3)
⇒at x=2 and t=4sec,∂y∂x=π
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 78
3 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 79
4 Videos
- DAILY PRACTICE PROBLEMSBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMSEXERCISE - dpp 76
5 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - Exercise
54 Videos
- ELASTICITY AND VISCOCITYBOOK - RESONANCECHAPTER - ELASTICITY AND VISCOCITYEXERCISE - Advanced Level Problems
9 Videos
Similar Questions
A sinusoidal wave propagates along a string. In figure (a) and (b) 'y' represents displacement of particle from the mean postion. 'x' & 't' have usual meanings. Find :-
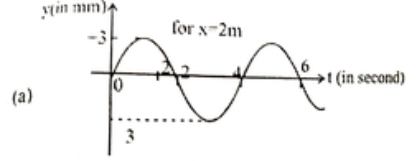
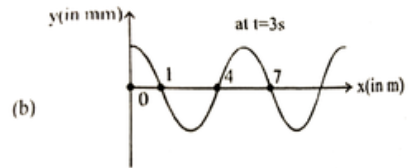
(a) wavelength, frequency and speed of the wave
(b) maximum velocity and maximum acceleration of the particles
View SolutionA sinusoidal wave having wavelength of 6m propagates along positive x direction on a string. The displacement (y) of a particle at x=2m varies with time (t) as shown in the graph
(a) Write the equation of the wave
(b) Draw y versus x graph for the wave at t=0

View Solution
Knowledge Check
A transverse wave passes through a medium, the maximum speed of the vibrating particle when the displacement of the particle from the mean position is
AzeroBequal to the amplitudeChalf of the amplitudeDmidway between mean and extreme positionA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.

Q. The velocity of propagation of the wave is ?A2cm/sB4cm/sC1cm/sD8cm/sA transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.
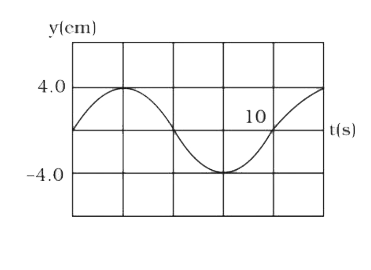
Q. Skecth of one wavelength of the wave (the portion between x=0 and x=20cm) at time t=0 is:A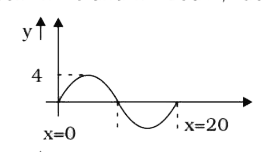 B
B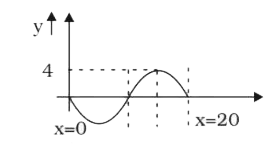 C
C D
D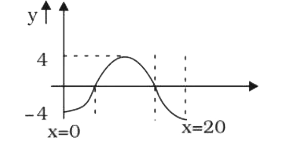
A transverse sinusoidal wave of wavelength 20 cm is moving along a string towards increasing x. the transverse displacement of the string particle at x=0 as a function of time is shown in figure.

Q. The velocity of propagation of the wave is ?
View SolutionA sinusoidal harmonic wave is propagating along a string stretched along x – axis. A particle on the string at x = 1 m is found to be at its mean position travelling in positive y direction at t=1s. The amplitude, wavelength and frequency of the wave are 0.01m,π2m and 20Hz respectively. Write the equation of the wave if-
(a) it is travelling along negative X direction
(b) it is travelling along positive X direction.
View SolutionA sinusoidal wave travels along a string. The time for a particular point to move from maximum placement to zero is 0.135s. What are the (a) period and (b) frequency? (c) The wavelength is 1. 40m, what is the wave speed?
View SolutionThe equation of a wave travelling on a string is y=(0.10mm)sin[(31.4m−1)x+(314s−1)t]
(a) In which direction does the travel?
(b) Find the wave speed, the wavelength and the frequency of the wave.
( c ) What is the maximum displacement and the maximum speed of a portion of the string?
View SolutionThe equation of a wave travelling on a string is y=(0.10mm)sin[(31.4m−1)x+(314s−1)t]
(a) In which direction does the travel?
(b) Find the wave speed, the wavelength and the frequency of the wave.
( c ) What is the maximum displacement and the maximum speed of a portion of the string?
View Solution
