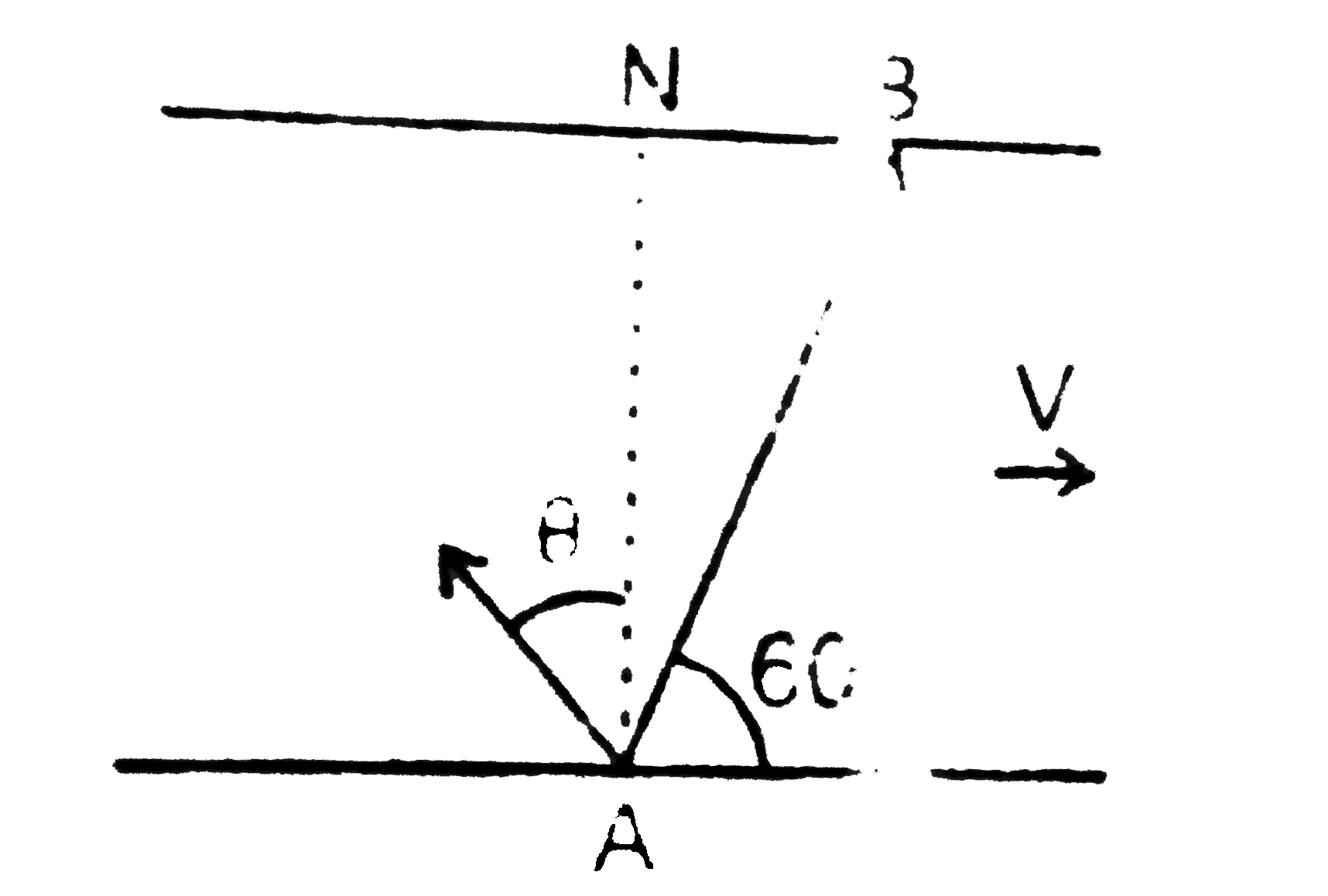
A swimmer wands to cross a river and reach point B directly from A. The speed of the wimmer in still river and that of river flow are same. The dotted line AN is normal to flow direction of river. For swimmer to reach point B, the angle his velocity relative to river will make with line AN is given by θ. then the value of θ is :
60∘
30∘
45∘
0∘
The correct Answer is:B
Since the speed of river flow and the person is same, the resultant direction AB is
such theta 90+θ2=60⇒θ=30∘
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.16
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.17
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.14
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
The speed of a swimmer with respect to the water is v, the speed of the stream is u. In what direction should the swimmer move to reach the opposite point on the other bank of the river? How long will he swim if the width of the river is l?
View SolutionA swimmer wants to cross a 600 m wide river . If the speed of swimmer is 12 km/hr in still water and speed of river is 6km/hr , along what direction the swimmer must strike in order to cross the river straight ? Also, calculate his resultant velocity and time taken by him to do so .
View Solution
Knowledge Check
If the speed of a swimmer in still water is 9 km/h. Find the down stream speed of the swimmer,whenthe river is flowing with the speed of 6 km/h.
A15 km/hB18 km/hC3 km/hD12 km/hA swimmer crosses a river of width d flowing at velocity v. While swimming, he keeps himself always at an angle of 120∘ with the river flow and on reaching the other end. He finds a drift of d/2 in the direction of flow of river. The speed of the swimmer with respect to the river is :
A(2−√3)vB2(2−√3)vC4(2−√3)vD(2+√3)vA swimmer wishes to cross a river 500m width flowing at a rate u. his speed w.r.t. still water is v. for this he makes an angle θ with the vertical as shown in the given figure then:
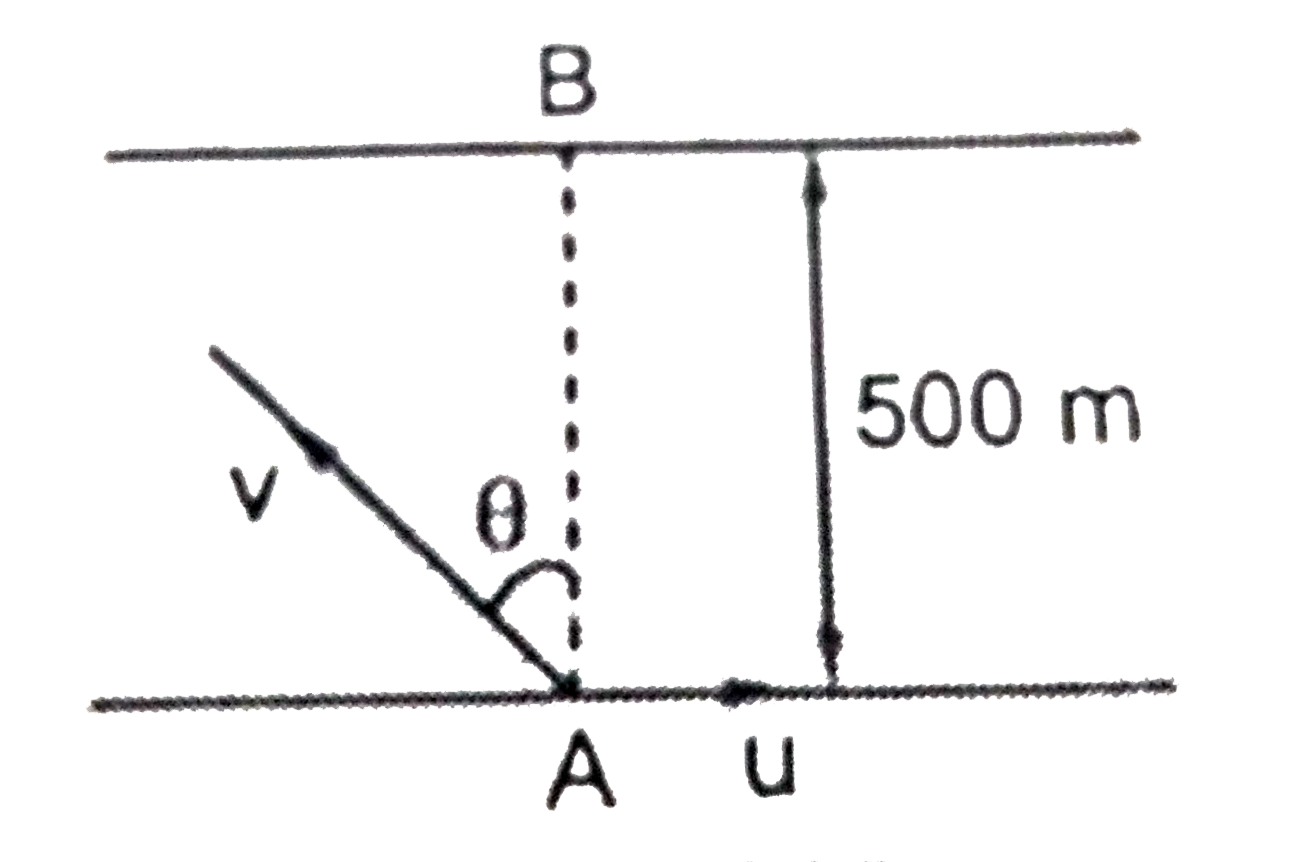 Ato cross the river in minimum time θ=0∘Bto cross the river in minumum time, θ=30∘Cfor u=3km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 6min.Dfor u=3 km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 3min.
Ato cross the river in minimum time θ=0∘Bto cross the river in minumum time, θ=30∘Cfor u=3km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 6min.Dfor u=3 km/hr and v=5km/hr, the time taken to cross the river in minimum time will be 3min.
A swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as hown. The velocity of the swimmer in still water is same as that of the water

(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity anf river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.
View SolutionA swimmer starts to swim from point a to cross a river. He wants to reach point B on the opposite side of the river. The line AB makes an angle 60∘ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water
(i) In what direction should he try to direct his velocity ? Calculate angle between his velocity ? Calculate angle between his velocity and river velocity.
(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

View SolutionA boat man can rown with a speed of 10kmh−1 in still water. If the river flows steadily at 5km/h, in which direction showld the boatman row in order to reach a point on the other bank directly opposite to the point from wher he stared ? The width of the river is 2km.
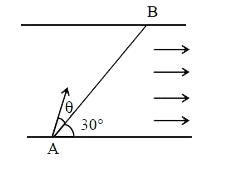
View SolutionA swimmer wants to cross a river from point A to point B. Line AB makes an angle of 30∘ with the flow of river. Magnitude of velocity of the swimmer is same as that of the river. The angle θ with the line AB should be _________ ∘, so that the swimmer reaches point B.
View SolutionA swimmer wishes to reach directly opposite bank of a river, flowing with velocity 8 m/s. The swimmer can swim 10 m/s still water. The width of the river is 480 m. Time taken by him to do so:
View Solution
