With what angular velocity the earth should spin in order that a body lying at 37∘ latitude may become weightless.
A
54√gR
B
2516√gR
C
53√gR
D
25g√gR
Video Solution
Text Solution
The correct Answer is:A
We have
mg'=mg−mω2Rcos2α
for weightless Net
0=mg−mω2Rcos2θ
⇒ω=√gR×1cosθ
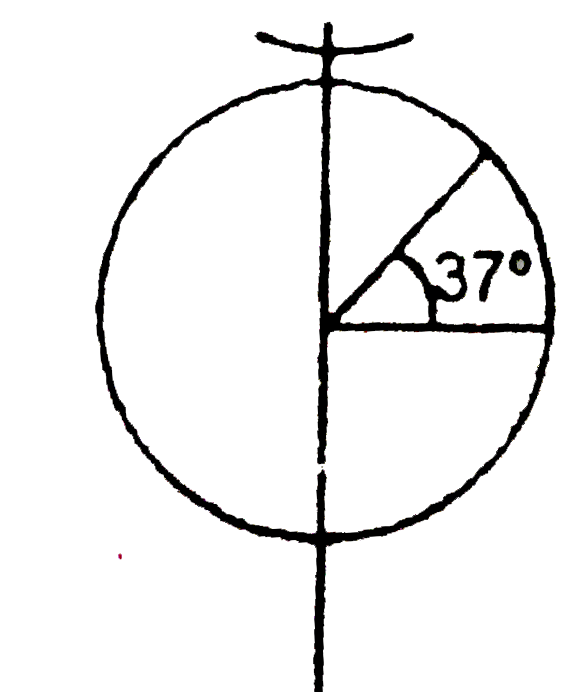
=√gR14/5=54√gR
|
Topper's Solved these Questions
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.24
9 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.25
20 Videos
- DAILY PRACTICE PROBLEMBOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.22
9 Videos
- CURRENT ELECTRICITYBOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)
21 Videos
- ELECTRO MAGNETIC WAVESBOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 3
27 Videos
Similar Questions
Knowledge Check
What is the angular velocity of the earth?
A2π86400rad/sB2π3600rad/sC2π24rad/sD2π6400rad/sCalculate angular velocity of the earth so that acceleration due to gravity at 60∘ latitude becomes zero (radius of the earth = 6400 km, gravitational acceleration at poles = 10m/s2,cos60∘=0.5)
A7.8×10−2 rad/sB0.5×10−3 rad/sC1×10−3 rad/sD2.5×10−3 rad/sThe weights of two objects one lying at the equator and the other at latitude 45∘ on earth and 100 N each. If the angular velocity of rotation of earth increases such that the object at the equator becomes weightless (zero N), the weight of the object at latitude 45∘ will be
A100 NB50 NC25 ND0 N
What is the angular velocity of a particle lying on the axis of rotation ?
View SolutionWith what angular velocity should a 20 m long cord be rotated such that tension in it, while reaching the highest point, is zero
View SolutionWhat should be the angular velocity of earth about its own axis so that the weight of the body at the equator would become 34 th of its present value ?
View SolutionThe angular velocity of earth at present is ω. What should be its angular velocity so that the body lying at the equator flies off
View SolutionThe angular velocity of the earth with which it has to rotate so that the acceleration due to gravity on 60∘ latitude becomes zero is
View Solution
