Two infinitely long line charges having charge density $λ$ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and $λ q > 0$ Neglect gravity. Find the time period.

Video Solution

Text Solution

Verified by Experts

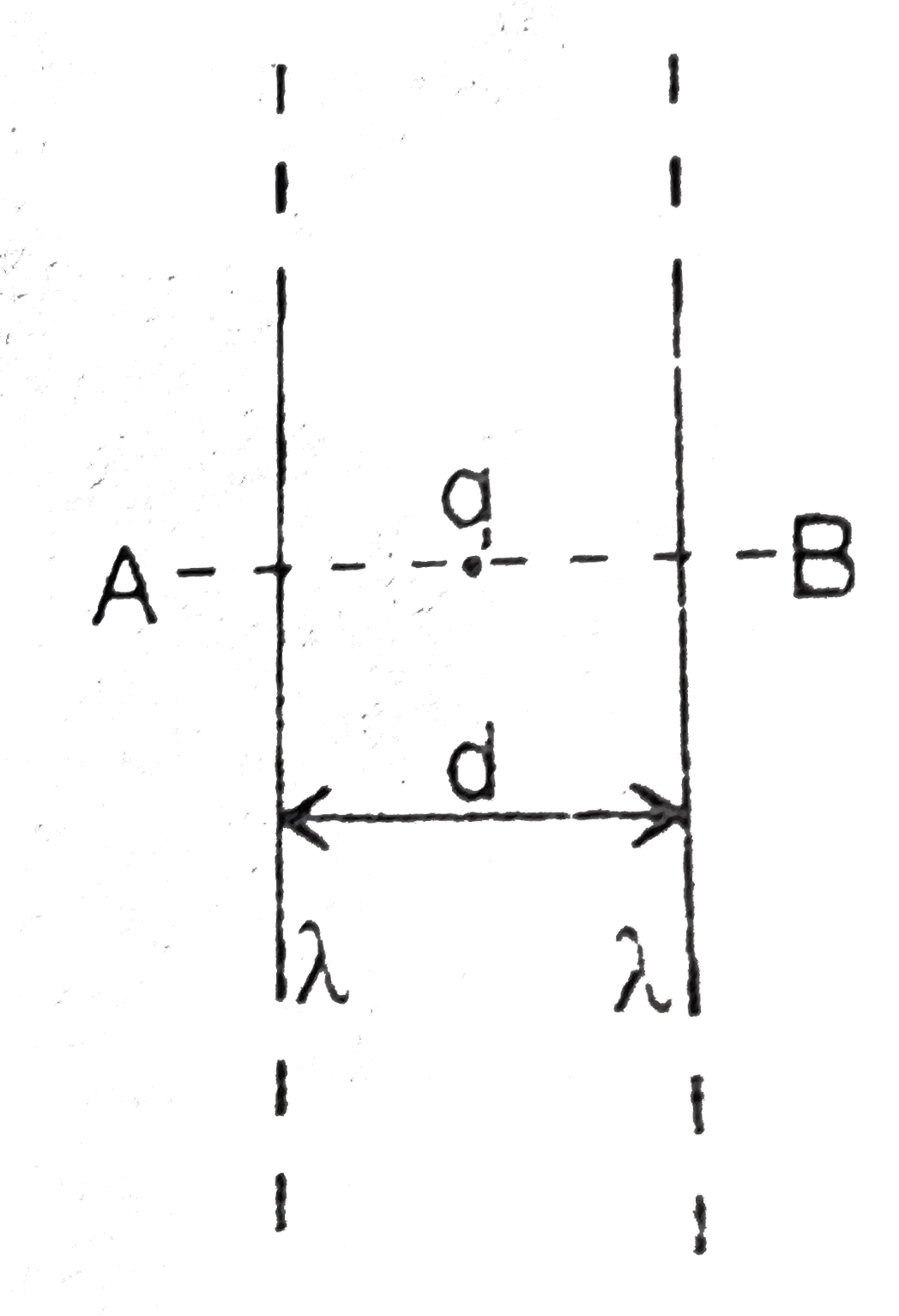
The correct Answer is: $2 π \sqrt{\frac{m d^{2} π \in_{0}}{4 λ q}}$

Two infinite plane parallel sheets separated by a distance d have equal and opposite uniform charge densities o. Electric field at a point between the sheets is
A $\frac{σ}{2 ε_{0}}$
B $\frac{σ}{ε_{0}}$
Czero
Ddepends on the location of the point
For an infinite line of charge having linear charge density $λ$ lying along x-axis the work done in moving a charge $q$ form $C$ to $A$ along $C A$ is

A $\frac{q λ}{2 π ε_{0}} In 2$
B $\frac{q λ}{2 π ε_{0}} In \sqrt{2}$
C $\frac{q λ}{4 π ε_{0}} In 2$
D $\frac{q λ}{2 π ε_{0}} In (0.5)$
Two infinite plane parallel sheets, separated by a distance d have equal and opposite uniform charge densities $σ$ . Electric field at a point between the sheets is
A $\frac{σ}{2 ε_{0}}$
B $\frac{σ}{ε_{0}}$
Czero
Ddepends on the location of the point