A cone made of a materal of relative density (d=2764) and height 4 m floats with its apex downward in a big container having water. Calculate the submerged height (in meter) of cone in water.
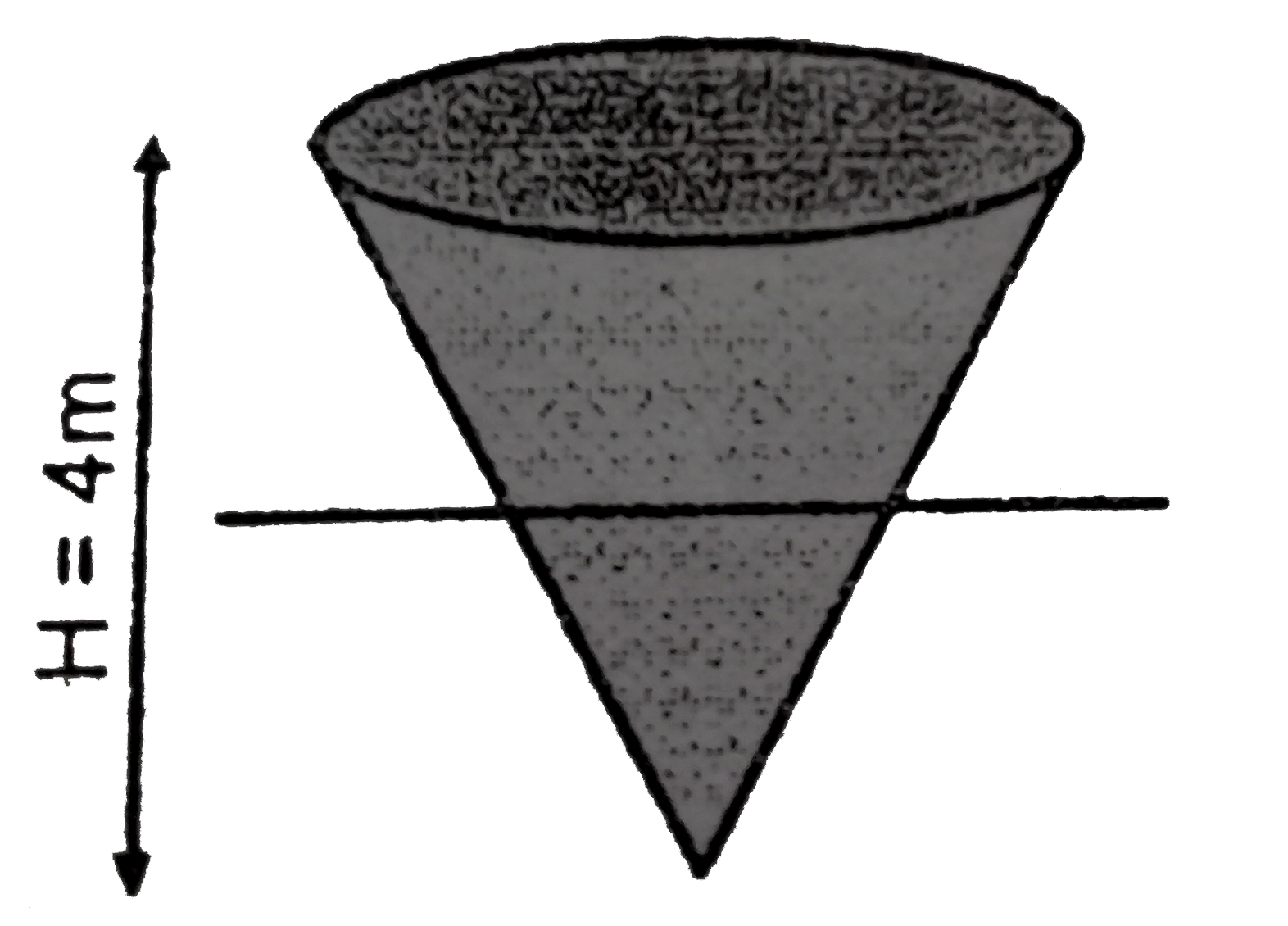
2 m
3 m
2.5 m
3.5 m
The correct Answer is:B
For floating condition buoyant force = weight
13A.(hH)2h.dwg=13(AH)dwd.g
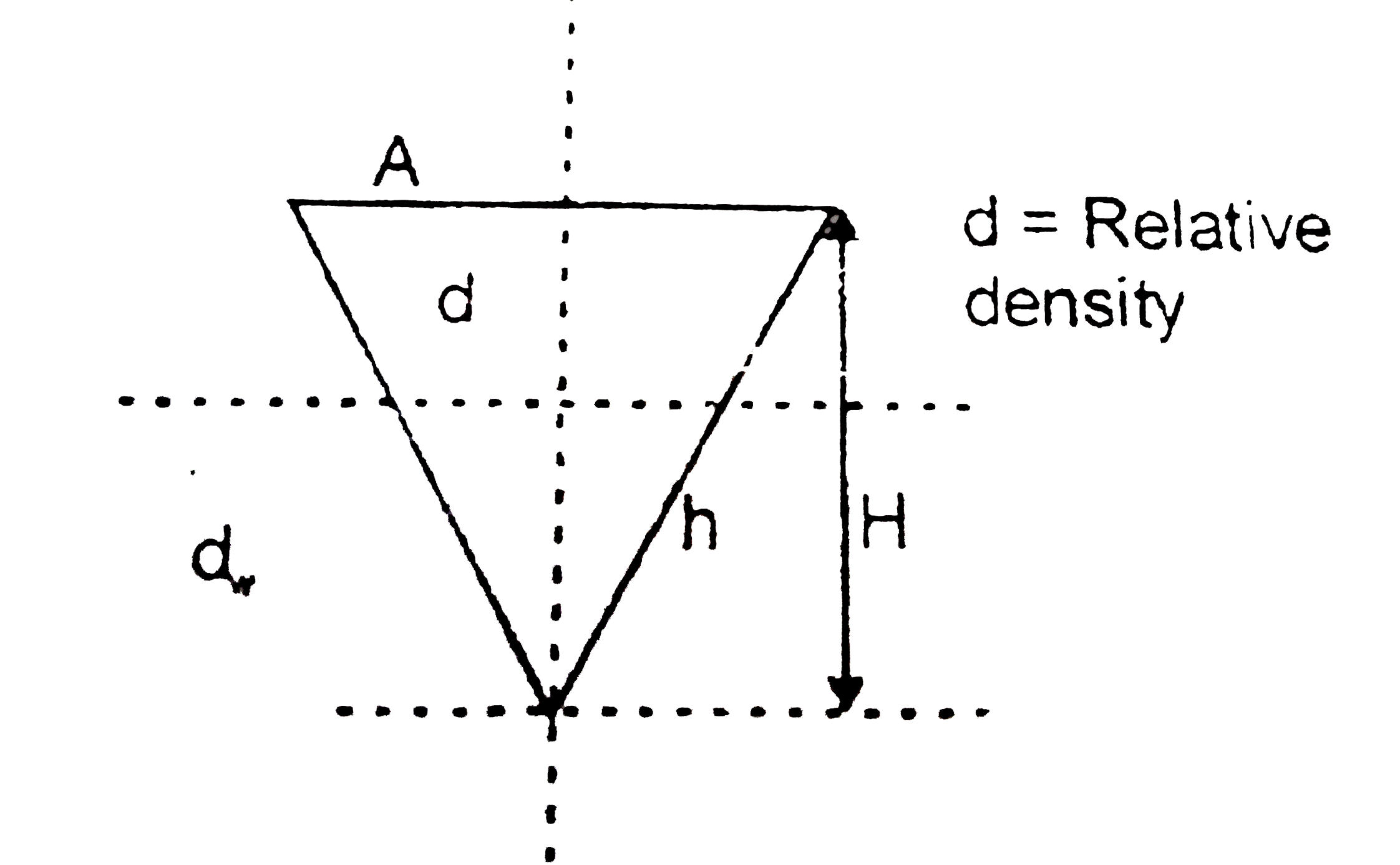
h=H(d)1/3=4(2764)1/3h=3m
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.3620videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.379videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - DAILY PRACTICE PROBLEMEXERCISE - DPP No.349videos
DAILY PRACTICE PROBLEM
- BOOK - RESONANCECHAPTER - CURRENT ELECTRICITYEXERCISE - High Level Problems (HIP)21videos
CURRENT ELECTRICITY
- BOOK - RESONANCECHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
A hole is made in the bottom of a container having water filled up to a height h. The velocity of water flowing out of the hole is :
Aindependent of h .Bproportional to h1/2Cproportional to hDproportional to h2 - Question 2 - Select One
A container is in the shape of an inverted cone. Its height is 6 m and radius is 4 m at the top. IF it is filled with water at the rate of 3m3/min, then the rate of change of height of water (inm/min) when the water level is 3 m is
A34πB29πC16πD2π - Question 3 - Select One
A uniform solid cone of mass m, base radius ‘R’ and height 2R, has a smooth groove along its slant height as shown in figure. The cone is rotating with angular speed ω, about the axis of symmetry. If a particle of mass ‘m’ is released from apex of cone, to slide along the groove, then angular speed of cone when particle reaches to the base of cone is
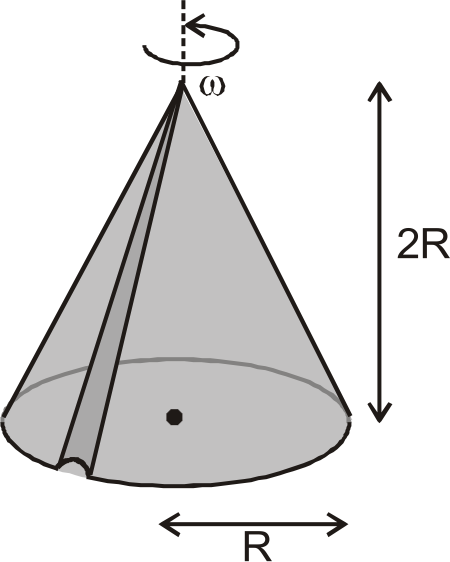 A3ω13B4ω13C5ω13D9ω13
A3ω13B4ω13C5ω13D9ω13
A hollow cone floats with its axis vertical upto one third of its height in a liquid in a liquid of relative density 0.8 and with its vertex submerged. When another liquid of relative density ρ is filled in it upto one third of its height, the cone floats upto half its vertical height. The height of the cone is 0.10m and the radius of the circular base is 0.05m. Find the specific gravity ρ is given.
View SolutionA solid is in the form of right circular cone surmounted on hemisphere of radius 4.2 cm and height of cone is 8 cm. The solid is placed in cylindrical tank full of water to submerge whole solid in water cylinder R=10cm , H= 19 . Find the volume of water left in cylinder.
View SolutionA cylindrical pot is slowly filled with. water. The centre of mass of the empty pot is at a height of 10cm, the mass of the pot is 1kg, and its inner area is 0.4m2. What is the height (in cm ) of the water in it, if the centre of mass of the system is at the lowest position? (Take density of water 1000kgm3 .
View SolutionA submarine 934 metres in height is floating on water.If 13 of its height is under water,then what is the height of the submarine visible above water?
View SolutionThe minimum slant height (in m) of a cone having volume 2√3 cubic meter is:
View Solution

