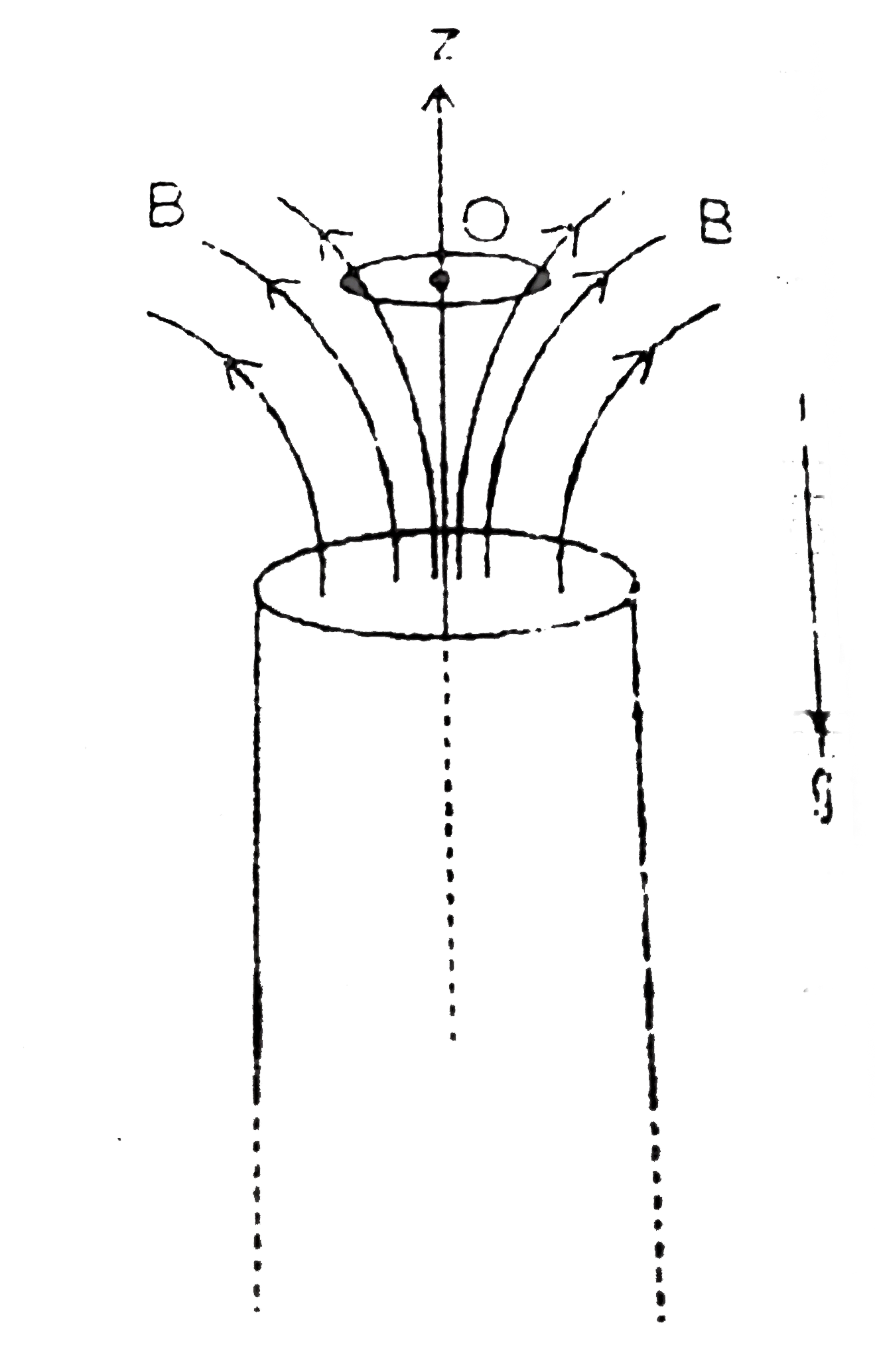
A thin superconducting (zero resistance) ring a held above a vertical long solenoid, as shown in the figure. The axis of symmetry of the ring is same to that of the solenoid. The cylindrically symmetric magnetic field around the ring can be described approximately in terms of the vertical and radial component of the magnetic field vector as $B_{z} = B_{0} (1 - α z)$ and $B_{r} = B_{0} β r$ , where $B_{0}, α$ and $β$ are positive constants, and z & r are vertical and radial position coordinates, respectively, Initially plane of the ring is horizontal has no current flowing in it. When relreased, it starts to move downwards with its axis axis still vertical. Initial coordinates of the centre of the ring 'O' is z = 0 and r =0. In the given diagram point O is on the axis and slightly above the solenoid having vertical and radial position coordinates as (0,0) Ring has mass m, radius m, radius $r_{0}$ and self inductance L. Assume the acceleration due to gravity as g.

Find the time period of SHM (for small displacement alon z-axis) of the ring.

$\frac{1}{B_{0} r_{0}^{2}} \sqrt{\frac{2 m L}{α β}}$

$\frac{1}{2 B_{0} r_{0}^{2}} \sqrt{\frac{2 m L}{α β}}$

$\frac{1}{B_{0} r_{0}^{2}} \sqrt{\frac{m L}{3 α β}}$

ring will not perform SHM

Text Solution

Verified by Experts

The correct Answer is:A

Total magnetic flux at any position
$ϕ = B_{z} π r_{0}^{2} - L I$
Since, $R = 0$ , so $ϕ = B_{0} (1 - α z) π r_{0}^{2} - L I =$ constant
From initial condition $(z = 0, I = 0)$ , the value of constant is $ϕ = B_{0} π r_{0}^{2}$
Using the above equation the current in the ring $I = \frac{1}{L} B_{0} α π r_{0}^{2} z$
The lorentz foce acting on the ring (which can only be vertical because of the symmetry of the assembly) can be expressed as)
$F_{z} = - B_{0} I (z) 2 π r_{0} = - \frac{2 B_{0}^{2} α β π^{2} r_{0}^{4} z}{L} = - k z$
Equation of motion of the ring is $m a_{z} = F_{z} - m g = - k z - m g$
Equilibrium position
$z_{0} = - m g / k ω_{0} = \sqrt{\frac{k}{m}}$ .

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Knowledge Check

A thin superconducting (zero resistance) ring a held above a vertical long solenoid, as shown in the figure. The axis of symmetry of the ring is same to that of the solenoid. The cylindrically symmetric magnetic field around the ring can be described approximately in terms of the vertical and radial component of the magnetic field vector as $B_{z} = B_{0} (1 - α z)$ and $B_{r} = B_{0} β r$ , where $B_{0}, α$ and $β$ are positive constants, and z & r are vertical and radial position coordinates, respectively, Initially plane of the ring is horizontal has no current flowing in it. When relreased, it starts to move downwards with its axis axis still vertical. Initial coordinates of the centre of the ring 'O' is z = 0 and r =0. In the given diagram point O is on the axis and slightly above the solenoid having vertical and radial position coordinates as (0,0) Ring has mass m, radius m, radius $r_{0}$ and self inductance L. Assume the acceleration due to gravity as g.

Find the vertical coordinates z for equilibrium position of the ring.
A $\frac{m g L}{2 B_{0}^{2} α β π^{2} r_{0}^{4}}$
B $- \frac{m g L}{2 B_{0}^{2} α β π^{2} r_{0}^{4}}$
Czero
Dnone of these
A thin superconducting (zero resistance) ring a held above a vertical long solenoid, as shown in the figure. The axis of symmetry of the ring is same to that of the solenoid. The cylindrically symmetric magnetic field around the ring can be described approximately in terms of the vertical and radial component of the magnetic field vector as $B_{z} = B_{0} (1 - α z)$ and $B_{r} = B_{0} β r$ , where $B_{0}, α$ and $β$ are positive constants, and z & r are vertical and radial position coordinates, respectively, Initially plane of the ring is horizontal has no current flowing in it. When relreased, it starts to move downwards with its axis axis still vertical. Initial coordinates of the centre of the ring 'O' is z = 0 and r =0. In the given diagram point O is on the axis and slightly above the solenoid having vertical and radial position coordinates as (0,0) Ring has mass m, radius m, radius $r_{0}$ and self inductance L. Assume the acceleration due to gravity as g.

Find the magnitude of current in the ring at a vertical position z.
A $\frac{1}{L} B_{0} α π r_{0}^{2} z$
B $\frac{1}{L} B_{0} α β π r_{0}^{2} z$
C $\frac{1}{2 L} B_{0} β π r_{0}^{2} z$
Dnone of these
The ring $B$ is coaxial with a solenoid $A$ as shown in figure. As the switch $S$ is closed at $t = 0$ , the ring $B$

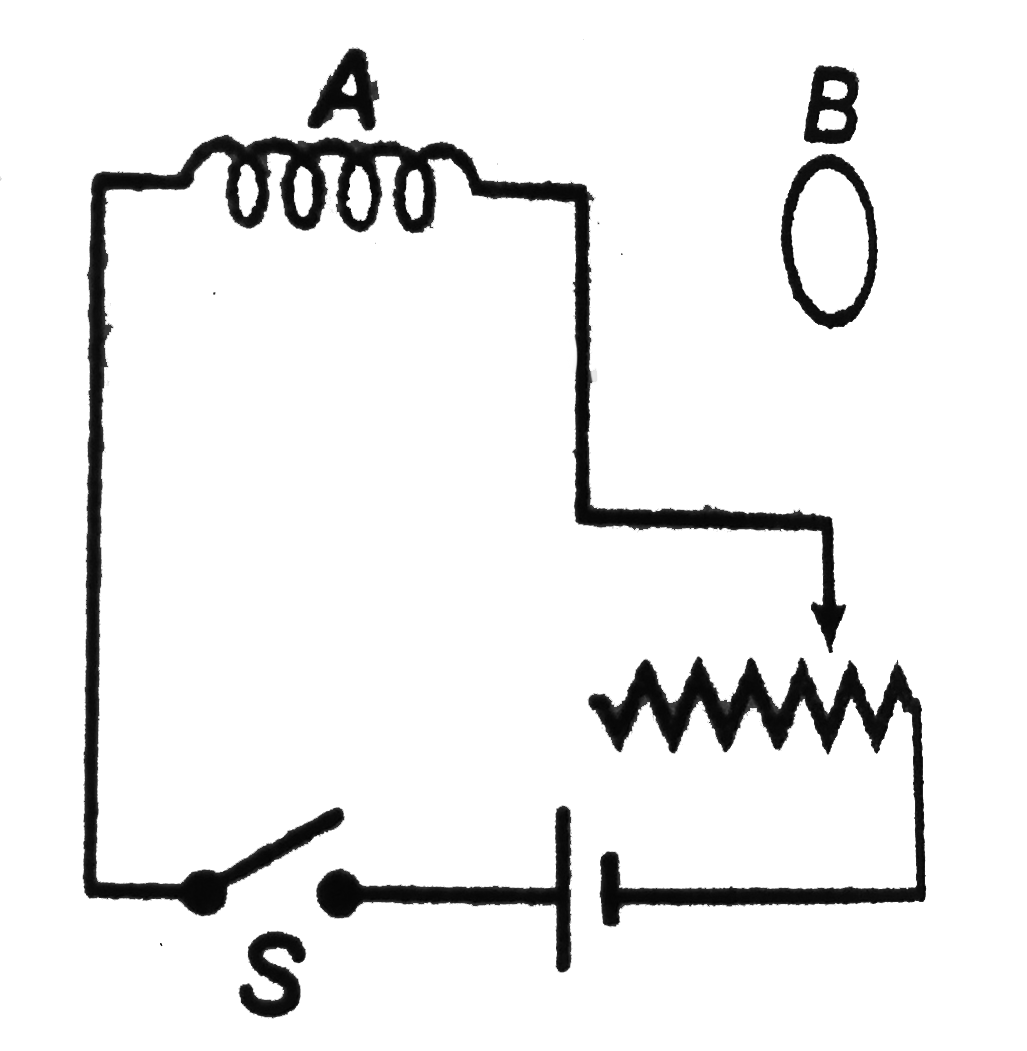Ais attracted towards AS
Bis repelled by A
Cis initially repelled and then attracted
Dis initially attracted and then repelled

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

The ring $B$ is coaxial with a solenoid $A$ as shown in figure. As the switch $S$ is closed at $t = 0$ , the ring $B$

RESONANCE-DAILY PRACTICE PROBLEM-DPP No.52

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

Knowledge Check

The ring B is coaxial with a solenoid A as shown in figure. As the switch S is closed at t=0, the ring B

RESONANCE-DAILY PRACTICE PROBLEM-DPP No.52

The ring $B$ is coaxial with a solenoid $A$ as shown in figure. As the switch $S$ is closed at $t = 0$ , the ring $B$