The resultant of two vectors →A and →B is perpendicular to →A and equal to half of the magnitud of →B. Find angle between →B and →B?
Video Solution
Text Solution
Since →R is perpendiuclar to →A.
fig shows the three vectors →A,→B and →R.
angle between →A and →B is π−θ
sinθ=RB=B2B=12
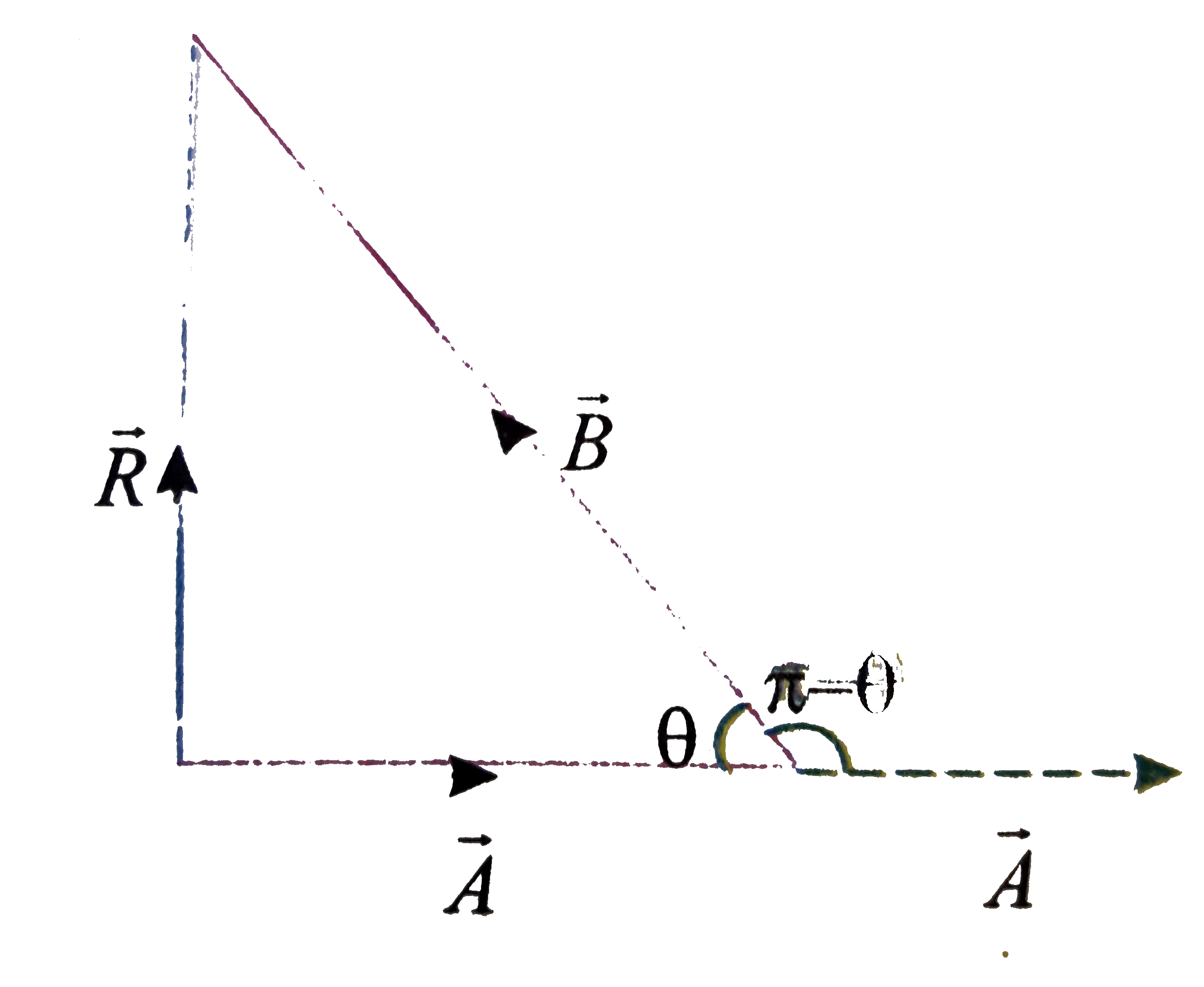
⇒θ=30∘
⇒ angle between →A and →B is 150∘
|
Topper's Solved these Questions
- VECTORSBOOK - NARAYNACHAPTER - VECTORSEXERCISE - C.U.Q
34 Videos
- VECTORSBOOK - NARAYNACHAPTER - VECTORSEXERCISE - LEVEL-I (C.W)
27 Videos
- UNITS AND MEASUREMENTSBOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - STATEMENT TYPE QUESTION
23 Videos
- WAVESBOOK - NARAYNACHAPTER - WAVESEXERCISE - Exercise-IV
56 Videos
Similar Questions
Knowledge Check
The resultant of the vectors A and B is perpendicular to the vector A and its magnitude is equal to half the magnitude of vector B. The angle between →A and →B is :-
A120∘B150∘C135∘DNone of theseThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitude is equal to half of the magnitude of the vector →B. Find out the angles between →A and →B.
 .A120B90C60D150
.A120B90C60D150The resultant of →A and →B is perpendicular to →A. What is the angle between →A and →B ?
Acos−1(AB)Bcos−1(−AB)Csin−1(AB)Dsin−1(−AB)
if →a,→band→c are mutally perpendicular vectors of equal magnitudes, then find the angle between vectors and →a+→b+→c.
View SolutionTwo vectors →A and →B have equal magnitudes. If magnitude of →A+→B is equal to n times the magnitude of →A−→B, then the angle between →A and →B is :-
View SolutionIf →a,→b are unit vectors such that the vector →a+3→b is peependicular to 7→a−→band→a−4→b is prependicular to 7→a−2→b then the angle between →aand→b is
View SolutionIf for two vector →A and →B, sum (→A+→B) is perpendicular to the difference (→A−→B). The ratio of their magnitude is
View SolutionThe resultant of two vectors →Aand→B is →C. If the megnitude of →B is doubled, the new resultant vector becomes perpendicular to →A, then the magnitude of →C is
View Solution
