Find the derivative of y with respect to x, when y=(3+mu)/(2+mu), wher

If $_{x} μ_{y}$ represents the refractive index when a ray of light goes from medium x to medium y , then the product $_{2} μ_{1} \times_{3} μ_{2} \times_{4} μ_{3}$ is equal to
A $_{2} μ_{1}$
B $\frac{1}{_{1} μ_{4}}$
C $_{3} μ_{2}$
D $_{4} μ_{2}$
In the figure shown $μ_{1}, μ_{2}, μ_{3}, μ_{4} and μ_{5}$ are the refractive indices

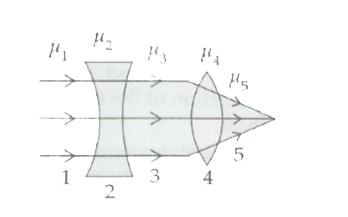
of the mediums 1,2,3,4 and 5 respectively . Consider the following
(1) $μ_{1} = μ_{2}$ (2) $μ_{3} = μ_{4} = μ_{5}$
$μ_{2} < μ_{3}$ (4) $μ_{4} > μ_{5}$
A1 and 2 only
B1, 2, and 3 only
C1 and 3 only
D3 and 4 only

Find the derivative of $y$ with respect to $x,$ when $y = \frac{3 + μ}{2 + μ},$ where $μ = {sin}^{- 1} x,$