Equation Of Sphere

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Equation of Sphere

Here, in this chapter, students would be able to learn about the equation of sphere. Here, we will also focus on the equation of sphere in standard form along with the surface area of the sphere and volume of a sphere.

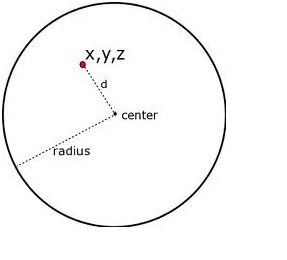
A geometrical object which is completely round in a three-dimensional space is called a sphere. The radius is the distance between the centre of the sphere to the outer point and is denoted by ‘r’. The diameter is denoted by ‘d’ which is the maximum straight distance between any two sides of the sphere through the centre.

sphere

What is a Hemisphere?

A hemisphere is the half of a sphere which is obtained where there is a split of sphere from the middle. It has the same radius and centre when it comes to the biggest circle of a sphere. On the other hand, coming to the great circle of a sphere, it has the same centre and radius as the sphere itself.

How is it possible to derive the Equation of a Sphere?

It is important to note that the equation of a sphere is given by

x2 + y2 = r2

It can be related to the algebraic method of starting the Pythagoras theorem.

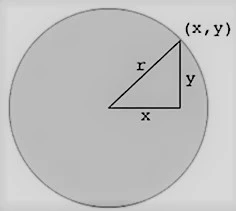
Sphere

Here, you can find that the point ( x, y ) lies on the triangle where |x| and |y| are the sides of the lengths of the right triangle where ‘r’ is the hypotenuse of the length. So, it can be written as,

x2 + y2 = r2

It should be noted that for the equation of a sphere, Pythagoras theorem can be used twice. Consider the figure below where O is the origin and P (x, y, z) is a point in three-dimensional space. On the sphere, there is ‘P’ where it has the radius ‘r’ when the distance from P to O is r

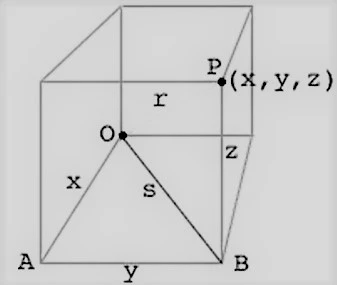
Pythagoras theorem (Sphere)

Here, we can find that x2 + y2 = s2 as OAB is a right-angle triangle. Here, you can find there is another triangle OBP and hence s2 + z2 = r2  So, here we can express the distance between O and P by:

x2 + y2 + z2 = |OP|2

x, y, z lies on the sphere where the radius is ‘r’ if

x2 + y2 + z2 = r2 This is called as the equation of a sphere.

If the centre of the sphere is ( a, b, c ), where the radius is represented by ‘r’ and the coordinates of the points on the surface of the sphere are ( x, y, z ), then we can find that the general equation of a sphere is (x – a)² + (y – b)² + (z – c)² = r²

What is the Volume of a Sphere Equation?

In order to calculate the volume of a sphere, the formula for it is given by:

The volume of the sphere = 43πr3 (Here r is the radius of the sphere)

What is the Surface Area of a Sphere Equation?

When there is a need to calculate the surface area of the sphere, the formula for it is given by:

The Surface area of the sphere= 4πr2 square units.

Related Videos:

Next, we will go through some of the solved examples to get all the clear idea in the best way.

Problem 1

The centre and radius of the sphere are given as (12, 7, -6) and 5 cm respectively. Determine the equation of the sphere in the standard form?

Solution:

Given:  Centre = (12, 7, -6) = (a, b, c)

Radius = 5 cm

We are already familiar that the equation of the sphere in the standard form is written as:

(x-a)2 + (y-b)2 + (z-c)2 = r2

Now, if we substitute the given values in the above form, we get:

(x-12)2 + (y-7)2 + (z -(-6))2 =52

(x-12)2 + (y-7)2 + (z +6)2 = 25

Thus, we can find that the equation of the sphere is (x - 12)2 + (y - 7)2 + (z + 6)2 = 25

Problem 2

The centre and radius of the sphere are given as (14, 8, -7) and 6 cm respectively. Determine the equation of the sphere in the standard form?

Solution:

Given:  Centre = (14, 8, -7) = (a, b, c)

Radius = 6 cm

We are already familiar that the equation of the sphere in the standard form is written as:

(x-a)2 + (y-b)2 + (z-c)2 = r2

Now, if we substitute the given values in the above form, we get:

(x-14)2 + (y-8)2 + (z -(-7))2 = 62

(x-14)2 + (y-8)2 + (z +7)2 = 36

Thus, the equation of the sphere is (x - 14)2 + (y – 8)2 + ( z + 7)2 = 36

Important Chapters:

Updated on:21/07/2023
|