The distributive law from algebra states that for all real numbers c,a1 and a2,we have c(a1+a2)=ca1+ca2 Use this law and mathematical induction to prove that,for all natural numbers,n≥2,if c,a1,a2,....,an are any real numbers,then c(a1+a2+.....+an)=ca1+ca2+....+can
Video Solution
Text Solution
Let P(n):c(a1+a2+…+an) = ca1+ca2+…+can ,for all natural numbers, n≥2.
Step1: For n=2,
P(2)
LHS= c(a1+a2)
RHS= ca1+ca2
As, it is given thatc(a1+a2) = ca1+ca2
Thus, P(2) is true.
Step2: For n=k,
Let P(k) be true
So, c(a1+a2+…+ak)= ca1+ca2+…+cak
Now, we need to show P(k+1) is true whenever P(k) is true.
P(k+1):
LHS= c(a1+a2+…+aK+ak+1)
=c[(a1+a2+…+ak)+ak+1]
=c(a1+a2+…+ak)+cak+1
=ca1+ca2++caK+cak+1
= RHS
Thus, P(k+1) is true, so by mathematical induction P(n) is true.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Suppose a1,a2,….are real numbers , with a1≠0 . If a1,a2,a3, ….are in A.P., then :
AA=⎡⎢⎣a1a2a3a4a5a6a5a6a7⎤⎥⎦ is singular (where i=√−1 )Bthe system of equations a1x+a2y+a3z=0 , a4x+a5y+a6z=0,a7x+a8y+a9z=0 has infinite number of solutionsCB=[a1ia2ia2a1] is nonsingularDNone of theseIf a1,a2,…,an are in HP, then the expression a1a2+a2a3+…+an−1an is equal to
A(n−1)(a1−an)Bna1anC(n−1)a1anDn(a1−an)The number of all three elements subsets of the set {a1,a2,a3….an} which contain a3 is
AnC3Bn−1C3Cn−1C2Dnone of these
If A1 and A2 be the two .Ms between two numbers 7 and 1/7 then (2A1−A2)(2A2−A1)=
View SolutionIf the line a1x+b1y+c1=0anda2x+b2y+c2=0 cut the coordinate axes in concyclic points, prove that : a1a2=b1b2.
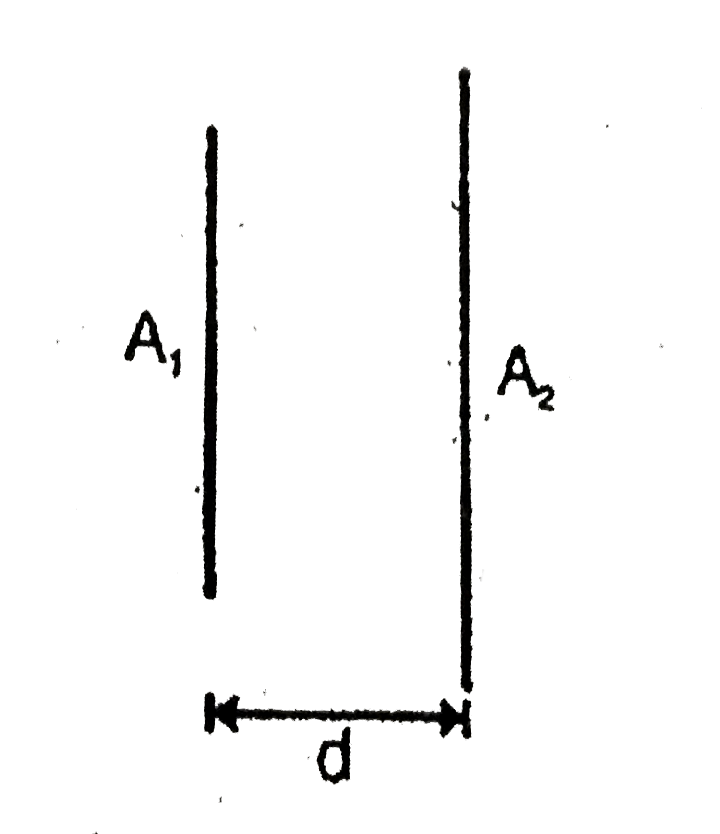
View SolutionThe capacitance of the capacitors of plate areas A1 and A2(A1<A2) at a distance d is
View SolutionIf a1,a2 …. an are positive real numbers whose product is a fixed real number c, then the minimum value of 1+a1+a2 +….. + an−1+an is :
View SolutionLet a1=0 and a1,a2,a3 …. , an be real numbers such that |ai|=|ai−1+1| for all I then the A.M. Of the number a1,a2,a3…., an has the value A where :
View Solution
