Find the LCM of 4! 5! and 6!
To find the LCM of 4!, 5!, and 6!, we can follow these steps:
Step 1: Calculate the factorials
First, we need to calculate the values of 4!, 5!, and 6!.
- 4!=4×3×2×1=24
- 5!=5×4!=5×24=120
- 6!=6×5!=6×120=720
Step 2: Write the factorials in terms of their prime factors
Next, we can express each factorial in terms of its prime factors.
- 4!=24=23×31
- 5!=120=23×31×51
- 6!=720=24×32×51
Step 3: Determine the LCM using the highest powers of each prime factor
To find the LCM, we take the highest power of each prime factor that appears in any of the factorials.
- For 2: The highest power is 24 (from 6!).
- For 3: The highest power is 32 (from 6!).
- For 5: The highest power is 51 (from both 5! and 6!).
Step 4: Calculate the LCM
Now we can calculate the LCM by multiplying these highest powers together:
LCM=24×32×51
Calculating this:
24=16,32=9,51=5
LCM=16×9×5
Calculating step-by-step:
1. 16×9=144
2. 144×5=720
Thus, the LCM of 4!, 5!, and 6! is 720.
Final Answer:
LCM(4!,5!,6!)=720
---
First, we need to calculate the values of 4!, 5!, and 6!.
- 5!=5×4!=5×24=120
- 6!=6×5!=6×120=720
Next, we can express each factorial in terms of its prime factors.
- 5!=120=23×31×51
- 6!=720=24×32×51
To find the LCM, we take the highest power of each prime factor that appears in any of the factorials.
- For 3: The highest power is 32 (from 6!).
- For 5: The highest power is 51 (from both 5! and 6!).
Now we can calculate the LCM by multiplying these highest powers together:
LCM=16×9×5
2. 144×5=720
LCM(4!,5!,6!)=720
Topper's Solved these Questions
Similar Questions
Find the LCM of 24 and 90.
View SolutionFind the LCM of 24 and 36.
View SolutionFind the LCM of 48 and 60
View SolutionFind the LCM of 144 and 156.
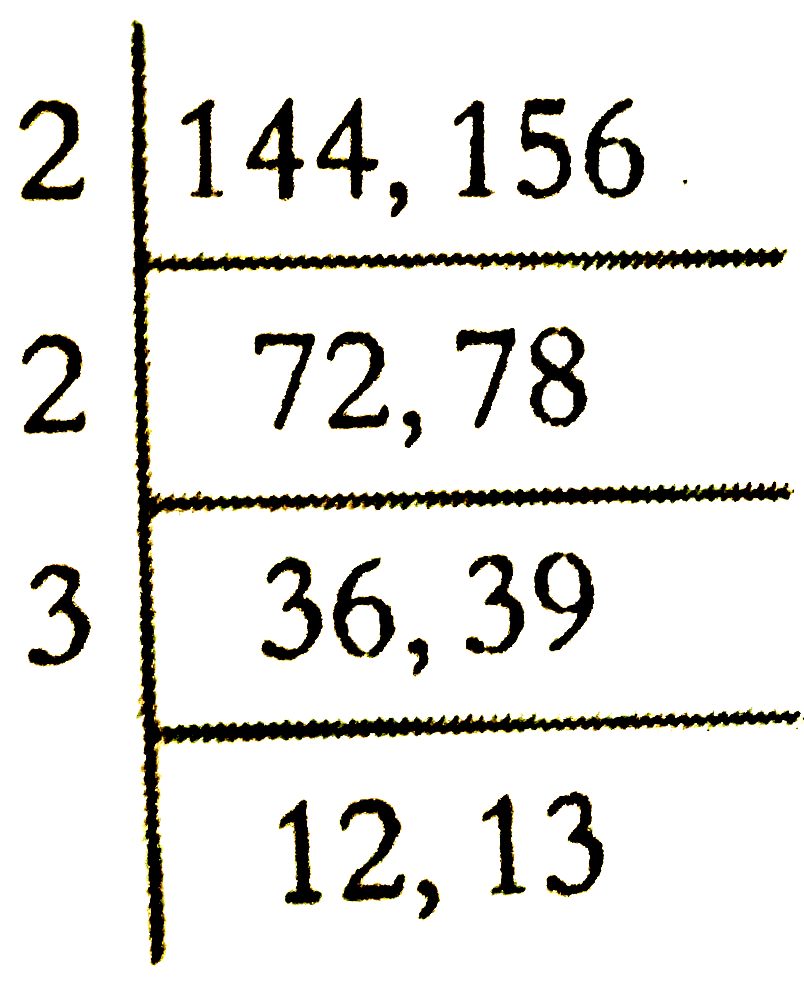 View Solution
View SolutionFind the LCM of 144 and 156.
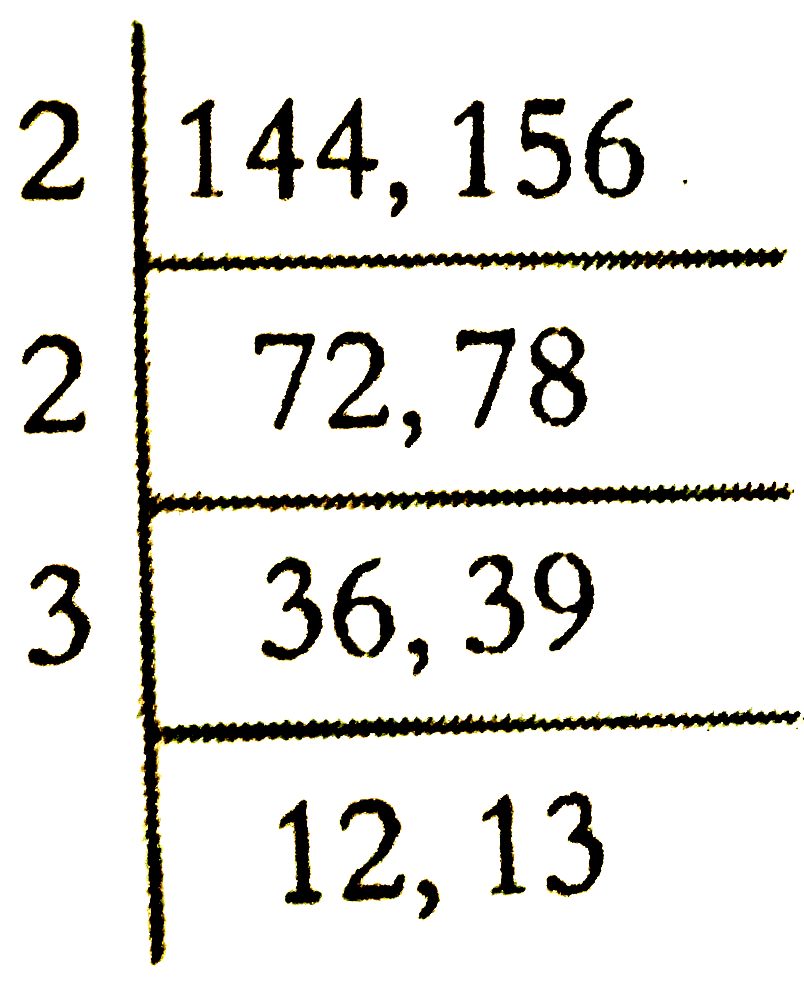 View Solution
View SolutionFind the LCM of 32 and 24.
View SolutionFind the LCM of 32 and 24.
View SolutionFind the LCM of 12 and 18
View SolutionFind the LCM of 4.44, 37 and 55.5 .
View SolutionFind the LCM of 4.44, 37 and 55.5 .
View Solution

