The number of diagonals that can be drawn by joining the vertices of an octagon is 20 b. 28 c. 8 d. 16
An octagon has 8 vertices.
The number of diagonals of a polygon is given by n(n−3)2
∴ Number of diagonals of an octagon
=8(8−3)2=20
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the number of diagonals which can be drawn by joining the angular points of a polygon of 100 sides?
A4850B4850C5000D10000
Find the number of diagonals formed by joining the vertices of the regular hexagon.
View SolutionFind the number of diagonals by joining the vertices of a polygon of n sides.
View SolutionNumber of quadrilaterals which can be constructed by joining the vertices of a convex polygon of 20 sides if none of the side of the polygon is also the side of the quadrilateral is: (a) 4825 (b)17C4−15C2 (c) 2275 (d) 2125
View SolutionSuppose 20 distinct points are placed randomly on a circle. Which of the following statements is/are correct?
1. The number of straight lines that can be drawn by joining any two of these points is 380.
2. The number of triangles that can be drawn by joining any three of these points is 1140.
View SolutionThere is a 25 sided polygon (not necessarily regular) inscribed in a circle. The maximum number of pentagons that can be made by using the vertices of the polygon is ? The maximum number of octagons that can be made by using the vertices of the polygon such that A5,A8&A13 are never used while A10andA20 are always used is ? The maximum number of triangles that can be made by using the vertices of the polygon such that there are atleast two but unequal number of vertices of the polygon between any two vertex of the triangle
View SolutionThe number of parabolas that can be drawn if two ends of the latus rectum are given 1 (b) 2 (c) 4 (d) 3
View SolutionA stop sign is an example of a Polygon. In the image , you can see examples of diagonals in geometry n the stop sign, there a various number of diagonals possible in a Polygon.

the number of diagonals (d) that can be drawn in polygons with a given number of sides (n) is being investigated.
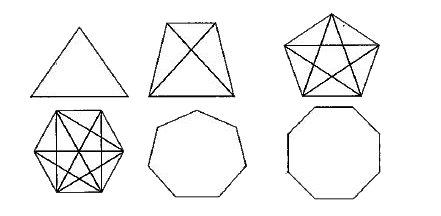

By considering the pattern, the value of 'p' is
View Solution
