Find the deviation from the mean and from median of the following distribution: Marks 0-10 10-20 20-30 30-40 40-50 No. of Students 5 8 15 16 6
To solve the problem of finding the deviation from the mean and from the median for the given distribution of marks and the number of students, we will follow these steps:
Step 1: Organize the Data
We have the following data:
| Marks (Class Interval) | No. of Students (Frequency) |
|------------------------|-----------------------------|
| 0-10 | 5 |
| 10-20 | 8 |
| 20-30 | 15 |
| 30-40 | 16 |
| 40-50 | 6 |
Step 2: Calculate the Midpoint (x_i) for Each Class Interval
The midpoint for each class interval is calculated as follows:
- For 0-10: x1=0+102=5
- For 10-20: x2=10+202=15
- For 20-30: x3=20+302=25
- For 30-40: x4=30+402=35
- For 40-50: x5=40+502=45
Step 3: Calculate the Total Frequency (N)
Now, we calculate the total number of students (N):
N=5+8+15+16+6=50
Step 4: Calculate fi⋅xi
Next, we calculate the product of frequency and midpoint for each class interval:
| Class Interval | Frequency (f_i) | Midpoint (x_i) | fi⋅xi |
|----------------|-----------------|-----------------|----------------------|
| 0-10 | 5 | 5 | 5⋅5=25 |
| 10-20 | 8 | 15 | 8⋅15=120 |
| 20-30 | 15 | 25 | 15⋅25=375 |
| 30-40 | 16 | 35 | 16⋅35=560 |
| 40-50 | 6 | 45 | 6⋅45=270 |
Now, summing fi⋅xi:
∑(fi⋅xi)=25+120+375+560+270=1350
Step 5: Calculate the Mean
Using the formula for the mean:
Mean=∑(fi⋅xi)N=135050=27
Step 6: Calculate the Deviation from the Mean
Now we calculate the absolute deviation from the mean for each midpoint:
- |x1−Mean|=|5−27|=22
- |x2−Mean|=|15−27|=12
- |x3−Mean|=|25−27|=2
- |x4−Mean|=|35−27|=8
- |x5−Mean|=|45−27|=18
Now, we multiply these deviations by their respective frequencies:
| Midpoint (x_i) | Deviation from Mean | Frequency (f_i) | fi⋅|xi−Mean| |
|----------------|----------------------|-----------------|-------------------------------|
| 5 | 22 | 5 | 5⋅22=110 |
| 15 | 12 | 8 | 8⋅12=96 |
| 25 | 2 | 15 | 15⋅2=30 |
| 35 | 8 | 16 | 16⋅8=128 |
| 45 | 18 | 6 | 6⋅18=108 |
Now summing these products:
∑(fi⋅|xi−Mean|)=110+96+30+128+108=472
Step 7: Calculate the Mean Deviation from the Mean
Using the formula for mean deviation:
Mean Deviation from Mean=∑(fi⋅|xi−Mean|)N=47250=9.44
Step 8: Calculate the Median
To find the median, we first need to find the cumulative frequency:
| Class Interval | Frequency (f_i) | Cumulative Frequency (CF) |
|----------------|-----------------|----------------------------|
| 0-10 | 5 | 5 |
| 10-20 | 8 | 13 |
| 20-30 | 15 | 28 |
| 30-40 | 16 | 44 |
| 40-50 | 6 | 50 |
Since N/2=25, the median class is the one where the cumulative frequency first exceeds 25, which is the class 20-30.
Step 9: Calculate the Median Using the Formula
Using the formula for the median:
Median=L+(N/2−CFf)⋅h
Where:
- L=20 (lower limit of the median class)
- CF=13 (cumulative frequency before the median class)
- f=15 (frequency of the median class)
- h=10 (class width)
Substituting the values:
Median=20+(25−1315)⋅10
=20+(1215)⋅10
=20+8=28
Step 10: Calculate the Deviation from the Median
Now we calculate the absolute deviation from the median for each midpoint:
- |x1−Median|=|5−28|=23
- |x2−Median|=|15−28|=13
- |x3−Median|=|25−28|=3
- |x4−Median|=|35−28|=7
- |x5−Median|=|45−28|=17
Now, we multiply these deviations by their respective frequencies:
| Midpoint (x_i) | Deviation from Median | Frequency (f_i) | fi⋅|xi−Median| |
|----------------|------------------------|-----------------|----------------------------------|
| 5 | 23 | 5 | 5⋅23=115 |
| 15 | 13 | 8 | 8⋅13=104 |
| 25 | 3 | 15 | 15⋅3=45 |
| 35 | 7 | 16 | 16⋅7=112 |
| 45 | 17 | 6 | 6⋅17=102 |
Now summing these products:
∑(fi⋅|xi−Median|)=115+104+45+112+102=478
Step 11: Calculate the Mean Deviation from the Median
Using the formula for mean deviation:
Mean Deviation from Median=∑(fi⋅|xi−Median|)N=47850=9.56
Final Results
- Mean Deviation from Mean: 9.44
- Mean Deviation from Median: 9.56
We have the following data:
|------------------------|-----------------------------|
| 0-10 | 5 |
| 10-20 | 8 |
| 20-30 | 15 |
| 30-40 | 16 |
| 40-50 | 6 |
The midpoint for each class interval is calculated as follows:
- For 0-10: x1=0+102=5
- For 10-20: x2=10+202=15
- For 20-30: x3=20+302=25
- For 30-40: x4=30+402=35
- For 40-50: x5=40+502=45
Now, we calculate the total number of students (N):
N=5+8+15+16+6=50
Next, we calculate the product of frequency and midpoint for each class interval:
|----------------|-----------------|-----------------|----------------------|
| 0-10 | 5 | 5 | 5⋅5=25 |
| 10-20 | 8 | 15 | 8⋅15=120 |
| 20-30 | 15 | 25 | 15⋅25=375 |
| 30-40 | 16 | 35 | 16⋅35=560 |
| 40-50 | 6 | 45 | 6⋅45=270 |
∑(fi⋅xi)=25+120+375+560+270=1350
Using the formula for the mean:
Mean=∑(fi⋅xi)N=135050=27
Now we calculate the absolute deviation from the mean for each midpoint:
- |x1−Mean|=|5−27|=22
- |x2−Mean|=|15−27|=12
- |x3−Mean|=|25−27|=2
- |x4−Mean|=|35−27|=8
- |x5−Mean|=|45−27|=18
| Midpoint (x_i) | Deviation from Mean | Frequency (f_i) | fi⋅|xi−Mean| |
|----------------|----------------------|-----------------|-------------------------------|
| 5 | 22 | 5 | 5⋅22=110 |
| 15 | 12 | 8 | 8⋅12=96 |
| 25 | 2 | 15 | 15⋅2=30 |
| 35 | 8 | 16 | 16⋅8=128 |
| 45 | 18 | 6 | 6⋅18=108 |
∑(fi⋅|xi−Mean|)=110+96+30+128+108=472
Using the formula for mean deviation:
Mean Deviation from Mean=∑(fi⋅|xi−Mean|)N=47250=9.44
To find the median, we first need to find the cumulative frequency:
| Class Interval | Frequency (f_i) | Cumulative Frequency (CF) |
|----------------|-----------------|----------------------------|
| 0-10 | 5 | 5 |
| 10-20 | 8 | 13 |
| 20-30 | 15 | 28 |
| 30-40 | 16 | 44 |
| 40-50 | 6 | 50 |
Using the formula for the median:
Median=L+(N/2−CFf)⋅h
Where:
- L=20 (lower limit of the median class)
- CF=13 (cumulative frequency before the median class)
- f=15 (frequency of the median class)
- h=10 (class width)
Median=20+(25−1315)⋅10
=20+(1215)⋅10
=20+8=28
Now we calculate the absolute deviation from the median for each midpoint:
- |x1−Median|=|5−28|=23
- |x2−Median|=|15−28|=13
- |x3−Median|=|25−28|=3
- |x4−Median|=|35−28|=7
- |x5−Median|=|45−28|=17
| Midpoint (x_i) | Deviation from Median | Frequency (f_i) | fi⋅|xi−Median| |
|----------------|------------------------|-----------------|----------------------------------|
| 5 | 23 | 5 | 5⋅23=115 |
| 15 | 13 | 8 | 8⋅13=104 |
| 25 | 3 | 15 | 15⋅3=45 |
| 35 | 7 | 16 | 16⋅7=112 |
| 45 | 17 | 6 | 6⋅17=102 |
∑(fi⋅|xi−Median|)=115+104+45+112+102=478
Using the formula for mean deviation:
Mean Deviation from Median=∑(fi⋅|xi−Median|)N=47850=9.56
- Mean Deviation from Mean: 9.44
- Mean Deviation from Median: 9.56
Topper's Solved these Questions
Similar Questions
Find the deviation from the mean and from median of the following distribution: Marks 0-10 10-20 20-30 30-40 40-50 No. of Students 5 8 15 16 6
View SolutionFind the mean deviation about arithmetic mean of the following frequency distribution.Marks 0−10,10−20,20−30,30−40,40−50 No. of Students 5,8,15,16,6
View SolutionCalculate the mean devation from the mean the following data:
Marks0−1010−2020−3030−4040−50No. of stu.5815166View SolutionFind the mean of the following frequency distribution: Class-interval: 0-10 10-20 20-30 30-40 40-50 No. of workers f: 7 10 15 8 10
View SolutionFind the mean deviation about median for the following data
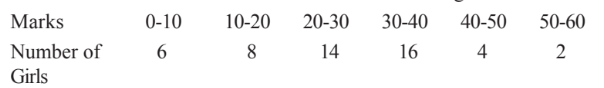 View Solution
View SolutionFind the mode of the following distribution of marks obtained by 80 students: Marks obtained 0-10 10-20 20-30 30-40 40-50 No. of students 6 10 12 32 20
View SolutionWrite the median class of the following distribution: Classes: 0-10 10-20 20-30 30-40 40-50 50-60 60-70 Frequency: 4 4 8 10 12 8 4
View SolutionFind the mean of the following frequency distributions: Class interval: 0-10 10-20 20-30 30-40 40-50 Frequency: 9 12 15 10 14
View SolutionCalculate mean deviation from the median for the following distribution: xi: 10 15 20 25 30 35 40 45 fi: 7 3 8 5 6 8 4 9
View SolutionCalculate mean deviation from the median for the following distribution: xi: , 10, 15, 20, 25, 30, 35, 40, 45 fi: , 7, 3, 8, 5, 6, 8, 4, 9
View Solution

