A battalion of soldiers is ordered to swim across a river wide. At what minimum rate should they swim perpendicular to river flow in order to avoid being washed away by the waterfall 300 m downstream. The speed of current being 3m/sec:
The correct Answer is:B
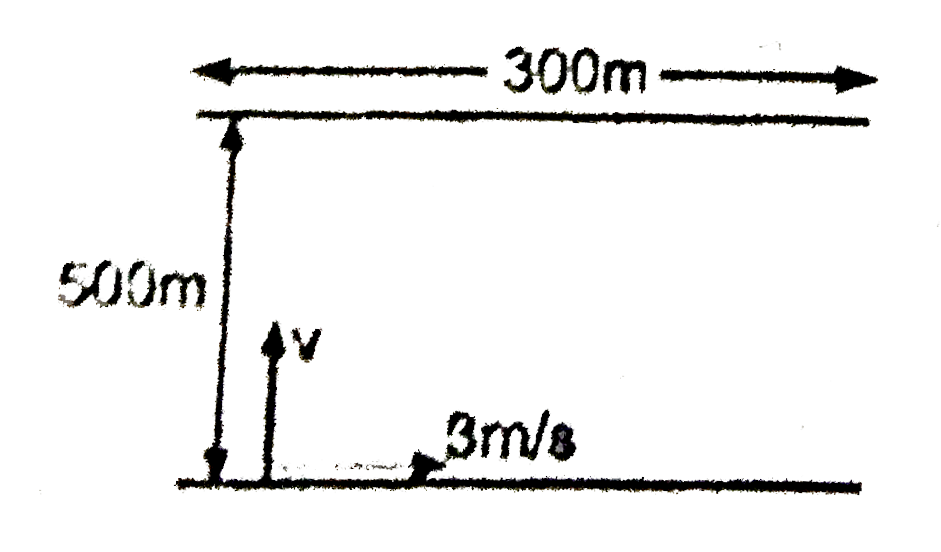
.
Topper's Solved these Questions
Similar Questions
A moan sinms across a river with speed of Vm perpendicular to the flow direction of river. If the water flows with a speed Vw with what resullant velocity does the man cross the river ?
View SolutionA man crosses a 320m wide river perpendicular to the current in 4 min. If in still water he can swim with a speed 5/3 times that of the current, then the speed of the current, in m/min is
View Solution
Knowledge Check
Assertion: To cross the river in minimum time swimmer should swimming in perpendicular direction to the water current.
Reason: In this case river flow helps to cross this river.AIf both assertion & Reason are True & the Reason is a corrrect explanation of the Asserion.BIf both Assertion & Reason are True but Reason is not correct explanation of the Assertion.CIf Assertion is Trie but the Reason is False.DIf both Assertion & Reason are falseA man wishes to swim across a river 0.5km. wide if he can swim at the rate of 2 km/h. in still water and the river flows at the rate of 1km/h. The angle (w.r.t. the flow of the river) along which he should swin so as to reach a point exactly oppposite his starting point, should be:-
AEBE/√2CE/2DzeroA man swims from a point A on the bank of a river if width 100m. When he swims perpendicular to the water current, he reaches the other bank 50m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is.
 .A10∘ upstreamB20∘ upstreamC30∘ upstreamD60∘ upstream
.A10∘ upstreamB20∘ upstreamC30∘ upstreamD60∘ upstream
A swimmer wishes to .cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angleθ with the perpendicular as shown ip. the. figure.
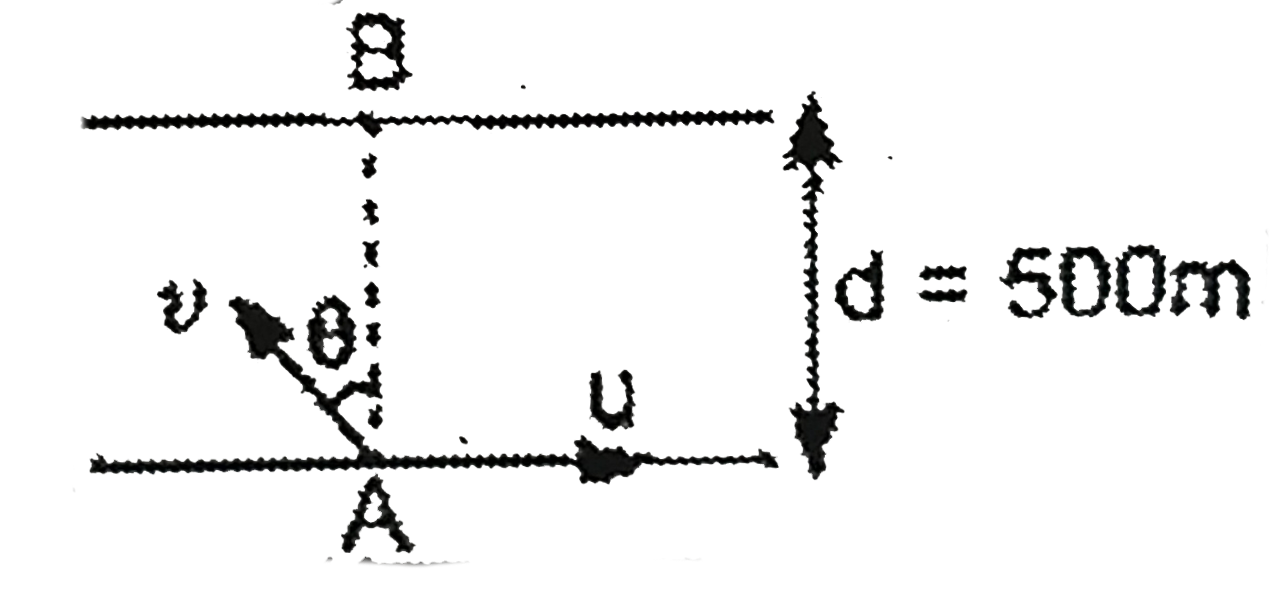
To cross the river in minimum time, the value of θ should be:
View Solutionman wants to swim across a river of which 200 m along the shortest path . If the speed of river stream is 3kmh−1 and speed of swimmer in still water is 5kmh−1 , then the time of crossing the river is
View SolutionA swimmer whishes to cross a river 500 m wide flowing at a rate 'u'. His speed with respect to still water is 'v'. For this, he makes an angle θ with the perpendicular as shown in the figure.

For u = 5 km/hrand v=3km//hr, the swimmer :
View SolutionA man can swim in still water at 4m/s river is flowing at 2m/s. the angle with downstream at which he should swim to cross the river minimum drift is
View SolutionA man wishes to swim across a river 40 m wide flowing with a speed of 3m/s. such that he reaches the point just infront on the other bank in time not greater than 100s. The angle made by the direction he swims and river flow direction is :-
View Solution
