A rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration

the normal reaction on the bead will be constant h magnitude and direction both
the magnitude of the normal reaction on the bead will be variable
the magnitude of friction force on the bead will be constant
the magnitude of friction force on the bead will be variable
The correct Answer is:D
due to α,ω is increasing
to overcome centripetal force mω2r the friction force will be variable
Topper's Solved these Questions
Similar Questions
A uniform rod of mass m and length l can rotate in a vertical plane about a smooth horizontal axis point H. a. Find angular acceleration α of the rod. just after it is released from initial horizontal position from rest'? b. Calculate the acceleration (tangential and radial) , point A at this moment.
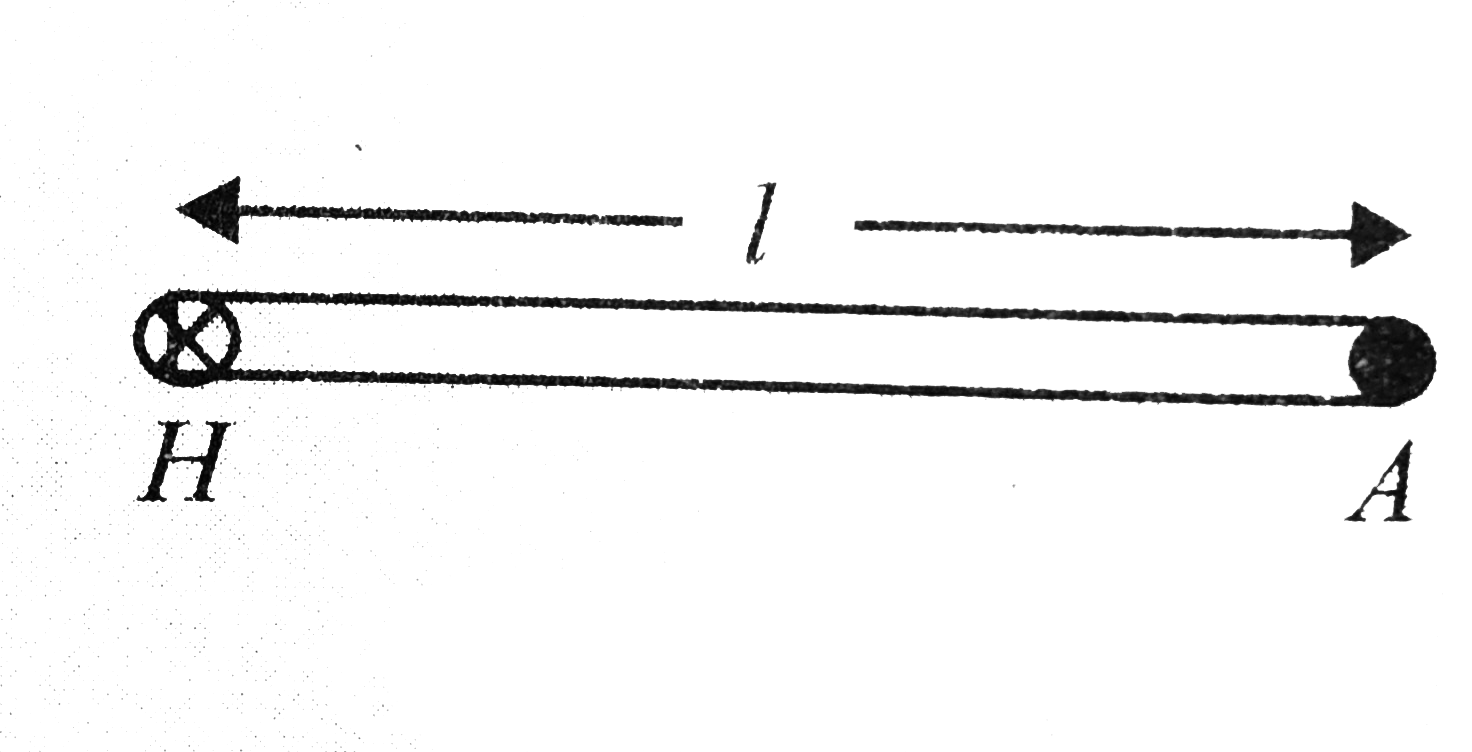 View Solution
View SolutionA copper rod AB of length l is rotated about one end A with a constant angular velocity ω. Calculate the electric field at a distance x from the axis of rotation. Also determine PD between A and B.
View Solution
Knowledge Check
- Question 1 - Select One
A long horizontal rod has a bead which can slide along its length and is initially placed at a distance L from one end A of the rod. The rod is set in angular motion about A with a constant angular acceleration, α. If the coefficient of friction between the rod and bead is μ, and gravity is neglected, then the time after which the bead starts slipping is :
A√μαBμ√αC1√μαDinfinitesimal - Question 2 - Select One
A long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping isA√μαBμ√αC1√μαDInfinitesimal - Question 3 - Select One
A long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping isA√μ/αBμ/√αC1√μαDinfinitesimal
A long horizontal rod has a bead which can slide along its length and initially placed at a

distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping isView SolutionA uniform metal rod is rotated in horizontal plane about a vertical axis passing through its end at uniform rate. The tension in the rod is
View SolutionThe figure shows a rod which startsm rotating with angular acceleration α about vertical axis passing through one of its end (A) in horizontal plane. A bead of mass m just fit's the rod and is situated at a distance 'r' from end A. Friction exists between rod and the bead with coefficient μ. As the angular velocity of rod increases the bead starts sliding over the rod (say after time t0)

Based on above information answer the following question :
Friction force acting on bead at time t(<t0) is given by :View SolutionThe figure shows a rod which startsm rotating with angular acceleration α about vertical axis passing through one of its end (A) in horizontal plane. A bead of mass m just fit's the rod and is situated at a distance 'r' from end A. Friction exists between rod and the bead with coefficient μ. As the angular velocity of rod increases the bead starts sliding over the rod (say after time t0)
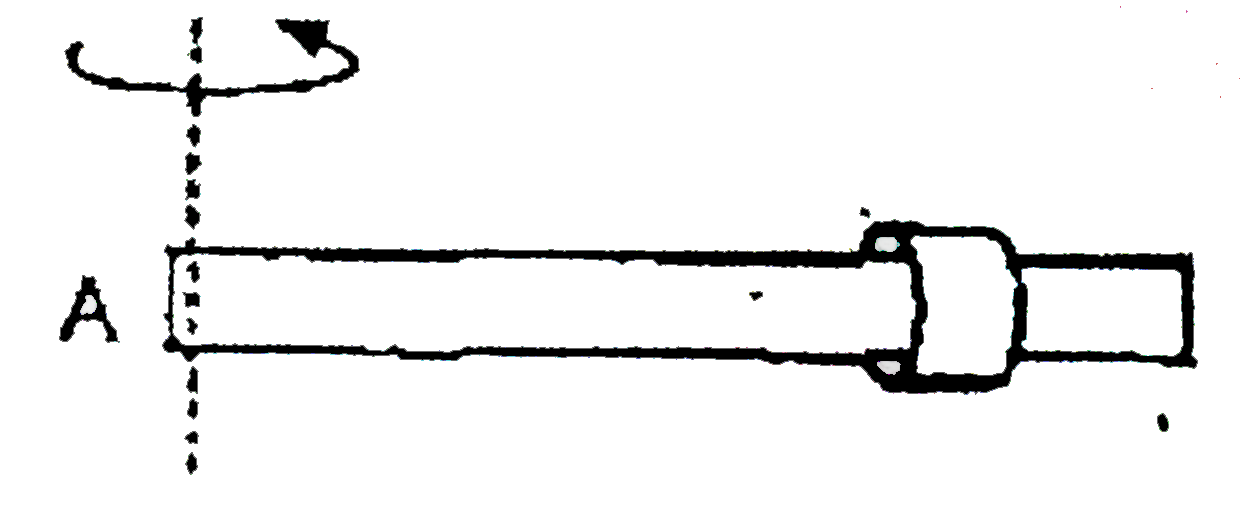
Based on above information answer the following question :
The normal force acting on bead at time t(<t0) is :View SolutionThe figure shows a rod which startsm rotating with angular acceleration α about vertical axis passing through one of its end (A) in horizontal plane. A bead of mass m just fit's the rod and is situated at a distance 'r' from end A. Friction exists between rod and the bead with coefficient μ. As the angular velocity of rod increases the bead starts sliding over the rod (say after time t0)
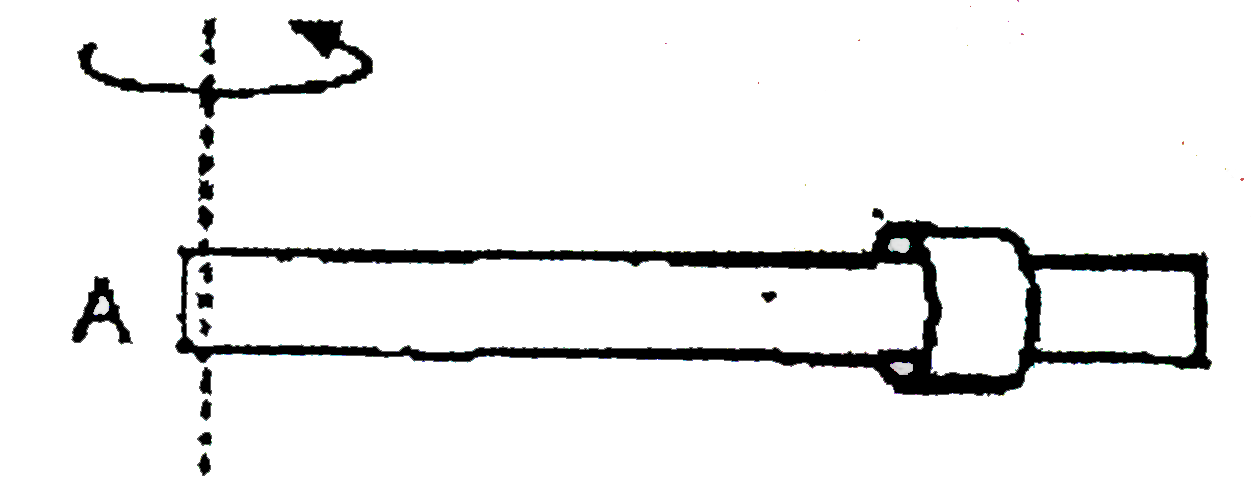
Based on above information answer the following question :
If the bead start sliding at t=t0 then value of t0 is given by :View Solution

