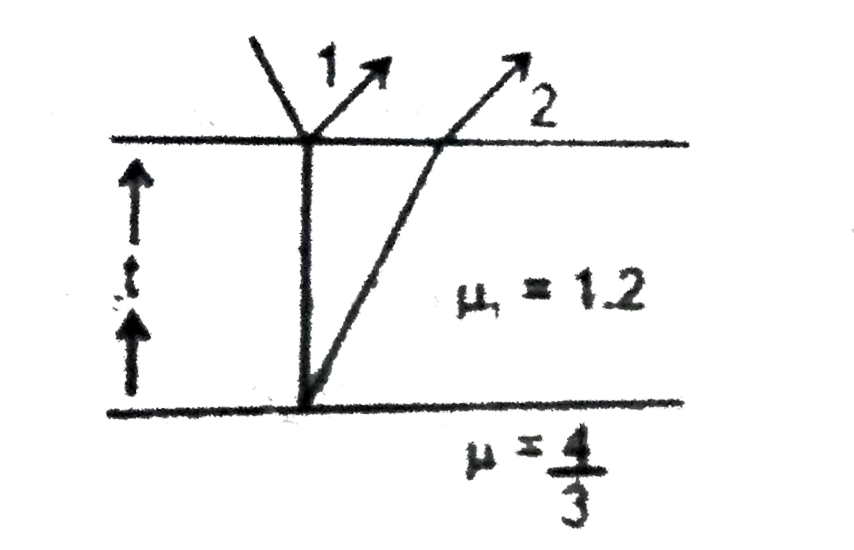
A thin oil film of refracting index 1.2 floats on the surface of water (μ=43). When a light of wavelength λ=9.6×10−7m falls normally on the film air, then it appears dark when seen normally. The minimum change in its thickness for which it will appear bright in normally reflected light by the same light is Z×10−7m. Then find Z.
10−7m
2×10−7m
3×10−7m
5×10−7m
The correct Answer is:B
For normal incidence path difference between ray 1 and ray 2 is 2μ1t
For minima thickness increment 2μ1Δt=λ2
⇒(t2−t1)=λ4μ1=9.6×10−74×1.2=2×10−7m
Topper's Solved these Questions
Similar Questions
A parallel beam of light of wavelength 560 nm falls on a thin film of oil (refractive index = 1.4). What should be the minimum thickness of the film so that it strongly S4 T z reflects the light ?
View SolutionWhite light is incident normally on a plane parallel thin film of µ=1.5. Find the minimum thickness of the film for which light of λ=4000 Å is absent from the reflected light
View Solution
Knowledge Check
A light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
A(a) 2.945×10−7mB(b) 3.945×10−7mC(c) 4.95×10−7mD(d) 1.945×10−7mA light of wavelength 5890Å falls normally on a thin air film. The minimum thickness of the film such that the film appears dark in reflected light is
A2.945×10−7mB3.945×10−7mC4.95×10−7mD1.945×10−7mA parallel beam of monochromatic light off wavelength λ=5×10−7m is incident normally on a single narrow slit of width 10−3mm. what is angle of diffraction, the first minimum if formed?
A30∘B45∘C60∘D75∘
White light is incident normally on a thin glass plate of refractive index 1.5. Calculate the minimum thickness of the film for which the wavelength 4200Å is absent for the reflected light.
View SolutionThe refractive index of glass with respect to water is 98. If the velocity of wavelength of light in glass are 2×108m/s and 4000 Å respectively, find the velocity and wavelength of light in water.
View SolutionDiffused monochromatic light with wavelength λ=0.60μm falls on a thin film with refractive index n=.5. Determine the film thickness if the angular separation of neighbouring maxima observed in reflected light at the amgles close to θ=45∘ to the normal is equal to ∂θ=3.0∘.
View SolutionThe outer surface of a transparent glass slab of refractive index μS=1.5 is coated by a thin layer of transparent medium of refractive index μC=1.6. Orange light of wavelength 6400Å falls normally on the coating. The reflected light at the upper surface and at the lower surface of teh coat interfere destructively. If thickness of the coat is 5K×10−8m, calculate the minimum value of K.
View SolutionA thin film of soap solution (μs=1.4) lies on the top of a glass plate (μg=1.5). When visible light is incident almost normal to the plate, two adjacent reflection maxima are observed at two wavelengths 420 and 630 nm. The minimum thickness of the soap solution is
View Solution
