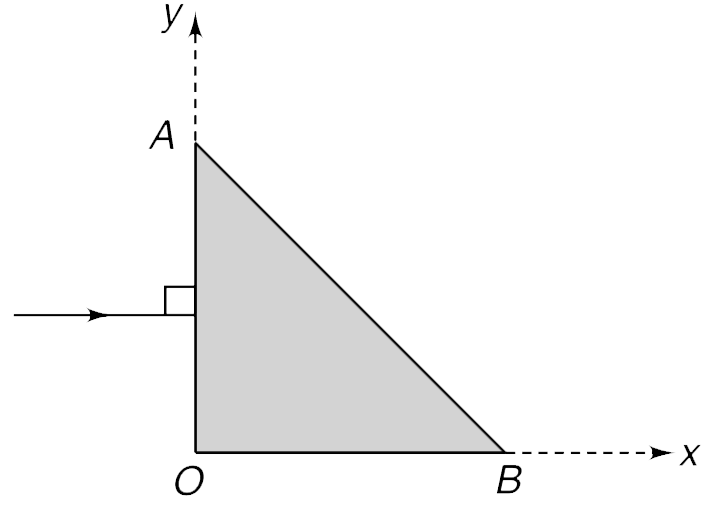
A triangular medium has varying refracting index n=n0+ax, where x is the distance (in cm) along x-axis from origin and n0=43. A ray is incident normally on face OA at the mid-point of OA. The range of a so that light does not escape through face AB when it falls first time on the face AB(OA=4cm, OB=3cm and AB=5cm): (Surrounding medium is air)
a>19
a>29
a>13
none of these
The correct Answer is:B
Clearly, PM=3/2 cm
37∘>sin−11n0+a(3/2)
35>1n0+3a2
3n0+9a2>5
9a2>1
a>29
Topper's Solved these Questions
Similar Questions
A triangular medium has varying refracting index μ=μ0+ax where x is the distance (in cm) along x-axis from origin and m0=4/3. A ray is incident normally on face OA at the mid-point of OA. Find the range of value of a so that light does not escape through face AB when it falls first time on the face AB.
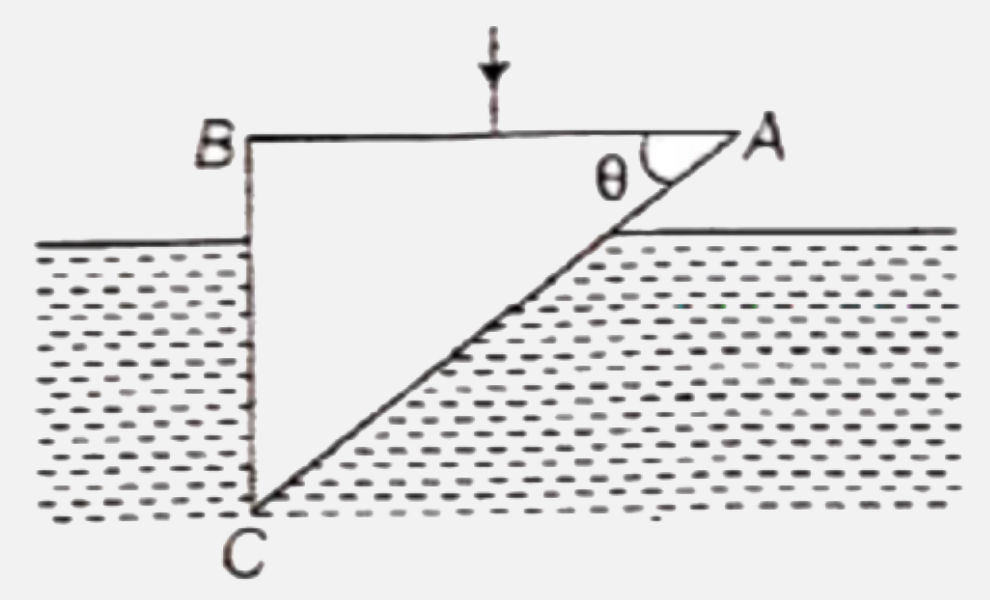
View SolutionA glass prims ABC (refractive index 1.5) , immersed in water (refrective index 43). A ray of light is incident normally one face AB. If it is totally reflected at the face AC, then
View Solution
Knowledge Check
- Question 1 - Select One
A glass prism is immeresed in water as shown in the figure. When a beam of light incident is incident normally on the face ab, it is internally reflected at the face ad. If the refractive index of glass is 1.5 and that of water is 4/3, then
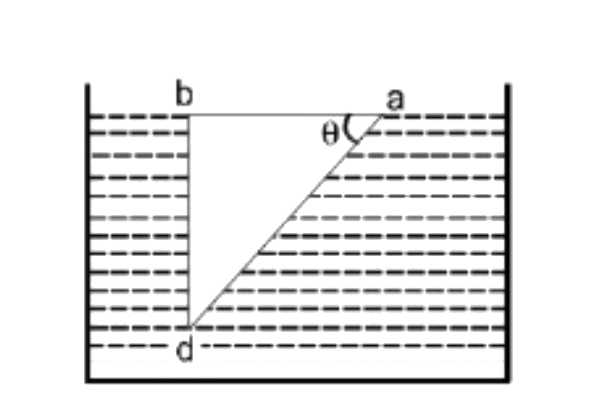Asinθ<(2/3)Bsinθ>(8/9)C(2/3)<sinθ<(8/9)DNone of these - Question 2 - Select One or More
A light ray enters into a medium whose refractive index varies along the x-axis as n(x)=n0√1+x4 where n0=1. The medium is bounded by the plates x=0,x=1 & y=0. It the ray enters at the origin at an angle 30∘ with x-axis
Aequation of trajectory of the light ray is y=[√3+x−√3]Bequation of trajectory of the light ray is y=2[√3+x−√3]Cthe coordinate the point at which light ray comes out from the medium is [1,2(2−√3)]Dthe coordinate the point at which light ray comes out from the medium is [0,2(2−√3)] - Question 3 - Select One
An air bubble in a glass slab with refractive index 1.5 (near normal incidence) is 5cm deep when viewed from one surface and 3cm deep when viewed from the opposite face. The thickness (in cm) of the slab is
A12B16C8D10
A equilateral glass prism has a refractive index √(2) . A light ray is incident at 45^∘ on one face.Total deviation of ray after refraction from second surface is n times15^(0) where 'n' is
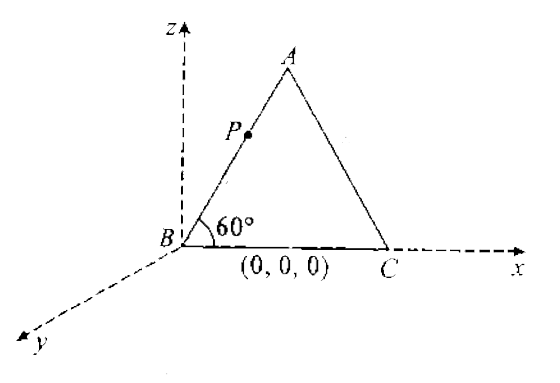
View SolutionAn equilateral prism ABC is placed in air with its base side BC lying horizontally along x-axis as shown in the figure. A ray given by √3z+x=10 is incident at a point P on the face AB of the prism
(a) Find the value μ from which the ray grazes the face AB
(b) Find the direction of the initially refracted ray if μ=32
(c) Find the equation of ray coming out of the prism if bottom BC is silvered ?
View SolutionA convex lens of focal length 15 cm and a concave mirror of focal length 30 cm are kept with their optic axis PQ and RS parallel but separated in vertical directiion by 0.6 cm as shown . The distance between the lens and mirror is 30 cm . An upright object AB of height 1.2 cm is placed on the optic axis PQ of the lens at a distance of 20 cm from the lens . if A'B' is the image after refraction from the lens and the reflectiion from the mirror , find the distance of A'B' from the pole of the mirror and obtain its magnification . Also locate positions of A' and B' with respect to the optic axis RS.
_E01_247_Q01.png)
View SolutionABC is a glass prism with ∠A=90° and other two angles 45° each
(a) Prove that any light ray that enters the prism through face AB will emerge out through the face AC if refractive index of the glass of the prism is μ≥√2 .
(b) A ray of light is incident parallel to BC at a height h = 3.0 cm from BC. Find the height above BC at which the emergent ray leaves the surface AC. It is given that μ=√2 and length BC=20cm. [Take tan15°0.25]View SolutionA light ray is incident on an irregular shaped slab of refractive index √2 at an angle of 45∘with the normal on the incline face as shown in the figure. The ray finally emerges from the curved surface in the medium of the refractive index μ=1.514 and passes through point E. If the radius of curved surface is equal to 0.4 m. find the distance OE correct upto two decimal places.
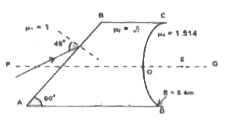View Solution