Students $I_{1}, J_{1}, J_{3}$ and $I_{2}$ perform an experiment for measuring the acceleration due to gravity (g) using a simple predulum, they use different lengths of the pendulum and record time for different number of oscillations. The observations are shown in the table. Least count for length $= 0.1 c m$ , least count for time = 1s
$\begin{matrix} Students & Length of the pendulum (cm) & No.of oscillations(n) & Time period of pendulum (s) I_{1} & 100.0 & 20 & 20 J_{1} & 400.0 & 10 & 40 J_{1} & 100.0 & 10 & 20 I_{1} & 400.0 & 20 & 40 \end{matrix}$
If $P_{1}, P_{2}, P_{3}$ and $P_{4}$ are the % error in g for students $I_{1}, J_{1}, J_{3}$ and $I_{2}$ respectively then -

$P_{1} = P_{3}$

$P_{3}$ is maximum

$P_{4}$ is minimum

$P_{a} = P_{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B, C

$T = 2 π \sqrt{\frac{l}{g}} \Rightarrow g \propto l T^{- 2} = \frac{Δ g}{g} = \frac{Δ l}{l} + \frac{2 Δ T}{T}$
Therefore $P = (\frac{Δ l}{l} + \frac{2 Δ T}{T}) 100 \Rightarrow P_{1} = (\frac{0.1}{100} + \frac{2 (1)}{400}) \times 100 = 0.6 % - P_{2} = (\frac{0.1}{400} + \frac{2 (1)}{400}) \times 100 = 0.42 %$
$P_{3} = (\frac{0.1}{100} + \frac{2 (1)}{200}) \times 100 = 1.1 %, P_{4} = (\frac{0.1}{400} + \frac{2 (1)}{800}) \times 100 = 0.28 %$ .

Updated on:21/07/2023

Class 11 PHYSICS DIMENSION AND MEASUREMENT

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Student I, II and III perform an experiment for measuring the acceleratioon due to gravity (g) using a simple pendulum . Theu use different lengths of the pedulum and /or record time for different number of oscillations . The observation are shoen in the table .
Least count for length =0.1cm
Least count for time =0.1s

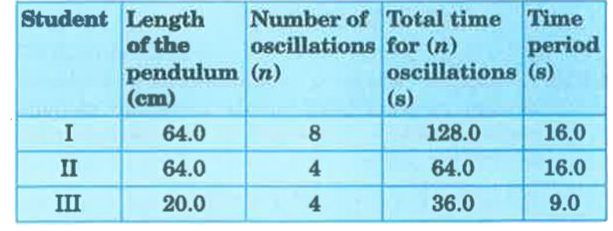
If $E_{I}$ , $E_{I I}$ and $E_{I I I}$ are the percentage errors in g,i.e
$\frac{Δ g}{g} \times 100$ for students I, II, and III respectively ,
A $E_{I} = 0$
B $E_{I}$ is minimum
C $E_{I} = E_{I I}$
D $E_{I I}$ is maximum
Question 2 - Select One
Student $I, I I, and I I I$ perform an experiment for measuring the acceleration due to gravity $(g)$ usinf a simple pendulum. They use lengths of the pendulum and // or record time for different number of oscillations . The observations are shown in the following table . Least count for length $= 0.1 c m$
$\begin{matrix} Student I I I I I I & Length of Pendulam (c m) 64.0 64.0 20.0 & Number of n Oscillation (n) 8 4 4 & Time Period (s) 16.0 16.0 9.0 \end{matrix}$
Least count for time $= 0.1 s$ .
If $E_{I}, E_{I I}$ , and $E_{I I I}$ are the percentage errors in $g$ , i.,e., $(\frac{Δ g}{g} \times 100)$ for students I,II , and III, respectively , then
A $E_{I} = 0$
B $E_{I} i s min i μ m$
C $E_{I} = E_{I I}$
D $E_{I I} i s max i μ m$
Question 3 - Select One
While measuring acceleration due to gravity by simpe pendulum a student makes a positive error of 1% in the length of the pendulum and a negative error of 3% in the value of the time period. His percentage error in the measurement of the value of g will be -
A $2 %$
B $4 %$
C $7 %$
D $10 %$

ALLEN-ERROR AND MEASUREMENT-Part-2(Exercise-2)(B)

Home
Ask Doubt
Profile

The correct Answer is:B, C

T=2π√lg⇒g∝lT−2=Δgg=Δll+2ΔTT Therefore P=(Δll+2ΔTT)100⇒P1=(0.1100+2(1)400)×100=0.6%−P2=(0.1400+2(1)400)×100=0.42% P3=(0.1100+2(1)200)×100=1.1%,P4=(0.1400+2(1)800)×100=0.28%.

Topper's Solved these Questions

Similar Questions

Knowledge Check

While measuring acceleration due to gravity by simpe pendulum a student makes a positive error of 1% in the length of the pendulum and a negative error of 3% in the value of the time period. His percentage error in the measurement of the value of g will be -

ALLEN-ERROR AND MEASUREMENT-Part-2(Exercise-2)(B)