A string of length L is stretched along the x-axis and is rigidly clamped at its two ends. It undergoes transverse vibration. If n an integer, which of the following relations may represent the shape of the string at any time :-
y=Asin(nπxL)cosωt
y=Asin(nπxL)sinωt
y=Acos(nπxL)cosωt
y=Acos(nπxL)sinωt
The correct Answer is:A, B
To solve the problem of finding the shape of a string of length L that is clamped at both ends and undergoes transverse vibrations, we can analyze the conditions required for the displacement of the string at its endpoints.
1. Understanding Boundary Conditions:
The string is clamped at both ends, which means that the displacement of the string at both ends (x = 0 and x = L) must be zero. Therefore, we have:
- At x = 0, y(0, t) = 0
- At x = L, y(L, t) = 0
2. General Form of the Solution:
The general form of the transverse vibration of a string can be expressed as:
y(x,t)=Af(x)g(t)
where f(x) is a function of position and g(t) is a function of time.
3. Applying the Boundary Conditions:
- For y(0,t)=0:
This implies that f(0)=0.
- For y(L,t)=0:
This implies that f(L)=0.
4. Choosing the Function f(x):
A common choice for f(x) that satisfies the boundary conditions is:
f(x)=sin(nπxL)
where n is an integer. This function equals zero at both x=0 and x=L.
5. Choosing the Function g(t):
The time-dependent part g(t) can be either cos(ωt) or sin(ωt). Thus, we can write:
g(t)=cos(ωt)org(t)=sin(ωt)
6. Formulating the Complete Solution:
Therefore, the complete solution for the shape of the string can be expressed as:
y(x,t)=Asin(nπxL)cos(ωt)(Option A)
or
y(x,t)=Asin(nπxL)sin(ωt)(Option B)
7. Evaluating Other Options:
- For y(x,t)=Acos(nπxL)cos(ωt): This does not satisfy the boundary conditions since at x=0, y(0,t)=A which is not zero.
- Therefore, this option is incorrect.
Conclusion:
The correct relations that represent the shape of the string at any time are:
- Option A: y(x,t)=Asin(nπxL)cos(ωt)
- Option B: y(x,t)=Asin(nπxL)sin(ωt)
The string is clamped at both ends, which means that the displacement of the string at both ends (x = 0 and x = L) must be zero. Therefore, we have:
- At x = 0, y(0, t) = 0
- At x = L, y(L, t) = 0
The general form of the transverse vibration of a string can be expressed as:
y(x,t)=Af(x)g(t)
where f(x) is a function of position and g(t) is a function of time.
- For y(0,t)=0:
This implies that f(0)=0.
- For y(L,t)=0:
This implies that f(L)=0.
A common choice for f(x) that satisfies the boundary conditions is:
f(x)=sin(nπxL)
where n is an integer. This function equals zero at both x=0 and x=L.
The time-dependent part g(t) can be either cos(ωt) or sin(ωt). Thus, we can write:
g(t)=cos(ωt)org(t)=sin(ωt)
Therefore, the complete solution for the shape of the string can be expressed as:
y(x,t)=Asin(nπxL)cos(ωt)(Option A)
or
y(x,t)=Asin(nπxL)sin(ωt)(Option B)
- For y(x,t)=Acos(nπxL)cos(ωt): This does not satisfy the boundary conditions since at x=0, y(0,t)=A which is not zero.
- Therefore, this option is incorrect.
The correct relations that represent the shape of the string at any time are:
- Option A: y(x,t)=Asin(nπxL)cos(ωt)
- Option B: y(x,t)=Asin(nπxL)sin(ωt)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-03)31videos
WAVES AND OSCILLATIONS
- BOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[A]29videos
WAVES AND OSCILLATIONS
- BOOK - ALLENCHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-01)53videos
WAVES AND OSCILLATIONS
- BOOK - ALLENCHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)51videos
SEMICONDUCTORS
Similar Questions
A string of length 1m stretched at both ends vibrating with frequency 300Hz which is 3 times the fundamental frequency
 View Solution
View SolutionA string of length 2x is stretched by 0.1 x and the velocity of a transverse wave along it is v. When it is stretched by 0.4x , the velocity of the wave is
View Solution
Knowledge Check
- Question 1 - Select One
A string of length 1 is stretched along the x-axis and is rigidly clamped at x=0 and x=1. Transverse vibrations are produced in the string. For nth harmonic which of the following relations may represents the shape of the string at any time
(a) y=2Acosωtcos(nπxl)
(b) y=2Asinωtcos(nπxl)
(c)y=2Acosωtsin(nπxl)
(d) y=2Asinωtsin(nπxl)Ac onlyBc and d onlyCa onlyDa,b,c and d - Question 2 - Select One or More
A pendulum is made by attaching a ball at the end of a string (the other end of the string is attached to the ceiling). The ball is released from rest at the position shown at some angle ϕ. Which of the following vectors may represent the impulse delivered by the string to the ball from the time it is released unitl the ball is at the bottom of the swing when string becomes vertical
 A
A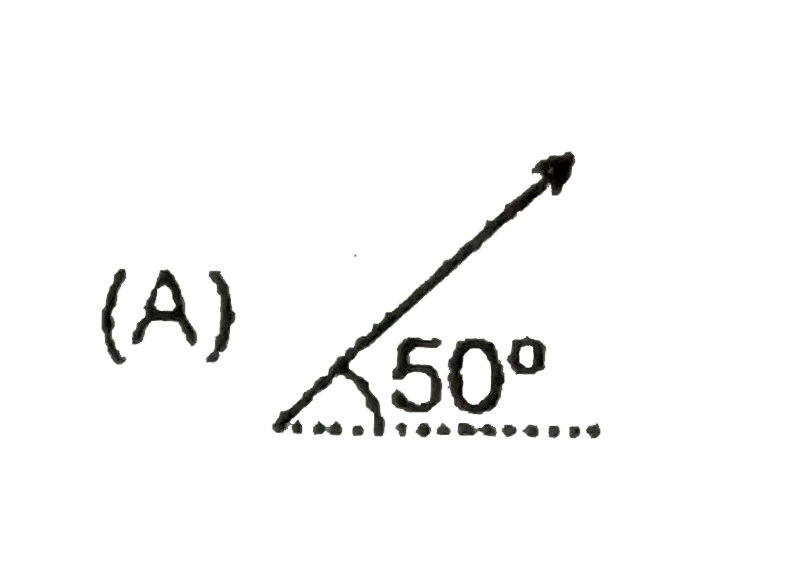 B
B C
C D
D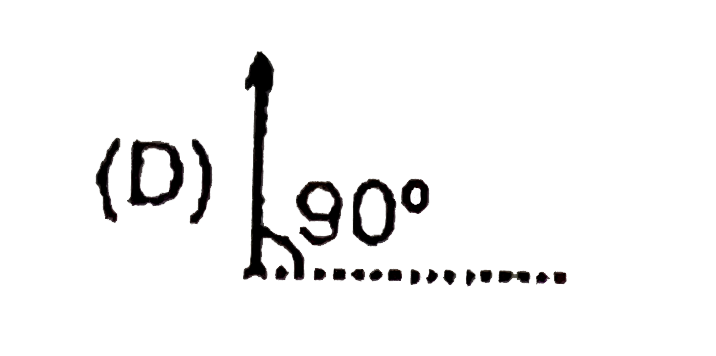
- Question 3 - Select One
A string is stretched within two rigid ends. It is vibrated in a node of first overtone. Which of the following is formed at a middle point of a string ?
AAntinodeBNodeCEither node or antinodeDNeither node nor antinode
A string is rigidly tied at two ends and its equation of vibration is given by y=cos2πx. Then minimum length of string is
View SolutionA string of length 2L, obeying Hooke's Law, is stretched so that its extension is L. The speed of the tranverse wave travelling on the string is v. if the string is futher stretched so that the extension in the string becomes 4L. The speed of transverse wave travelling on the string will be
View SolutionOne end of a taut string of length 3m along the x-axis is fixed at x=0. The speed of the waves in the string is 100ms−1. The other end of the string is vibrating in the y-direction so that stationary waves are set up in the string. The possible wavelength(s) of these sationary waves is (are)
View SolutionA string of length L fixed at both ends vibrates in its first overtone. Then the wavelength will be
View SolutionA string of length 0.4 m and mass 10−2 kg is clamped at its ends. The tension in the string is 1.6 N. When a pulse travels along the string the shape of the string is found to be the same at times t and t+△t. The value △t is
View Solution

