Suppose Q is a point on the circle with centre P and radius 1, as shown in the figure: R is a point outside the circle such that QR=1 and ∠QRP=2∘. Let S be the point where the segment RP intersects the given circle. Then measurement of ∠RQS equals
Step by step video & image solution for Suppose Q is a point on the circle with centre P and radius 1, as shown in the figure: R is a point outside the circle such that QR=1 and /_QRP=2^@. Let S be the point where the segment RP intersects the given circle. Then measurement of /_RQS equals by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
Circles with centres P and Q intersects at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circles are congruent, show that : CE = BD.
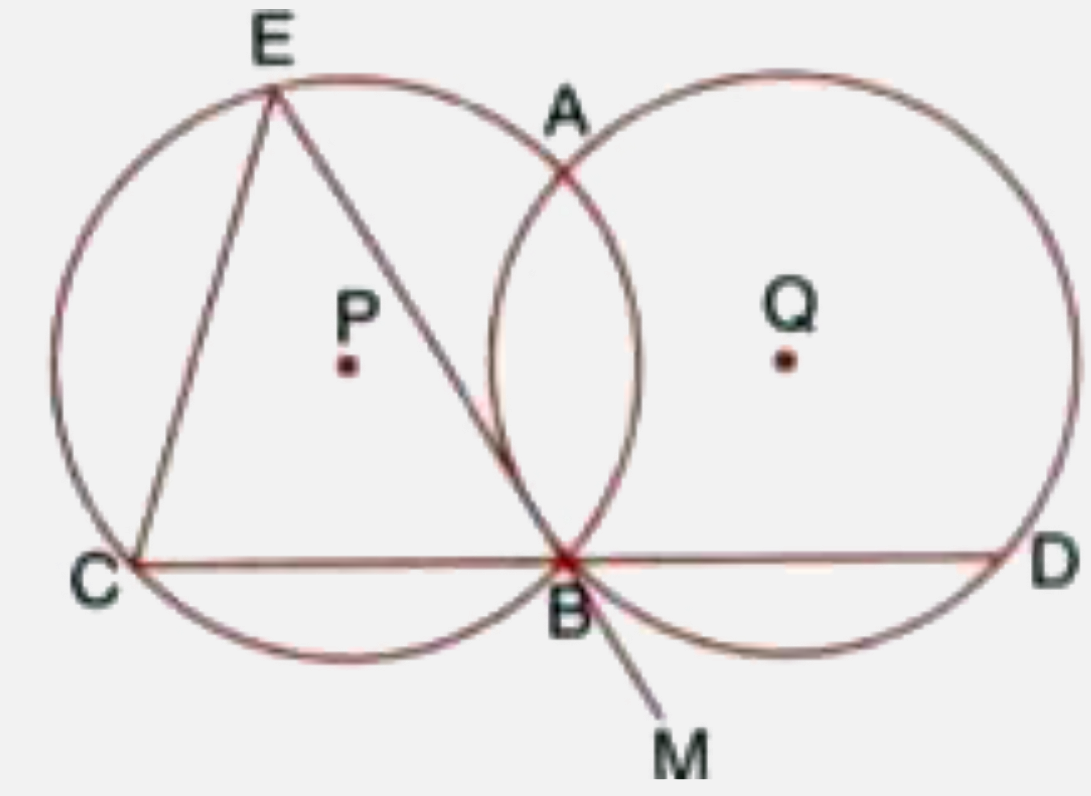
View SolutionTwo circles intersect at two points P and S. QR is a tangent to the two circles at Q and R. If ∠QSR=72∘, then ∠QPR=.
View Solution
Knowledge Check
Suppose Q is a point on the circle with center P and radius 1, as shown in the figure , R is a point outside the circle such that QR=1and∠QRP=2∘ . Let S be the point where the segment RP intersects the given circle. Then measure of ∠RQS equals-
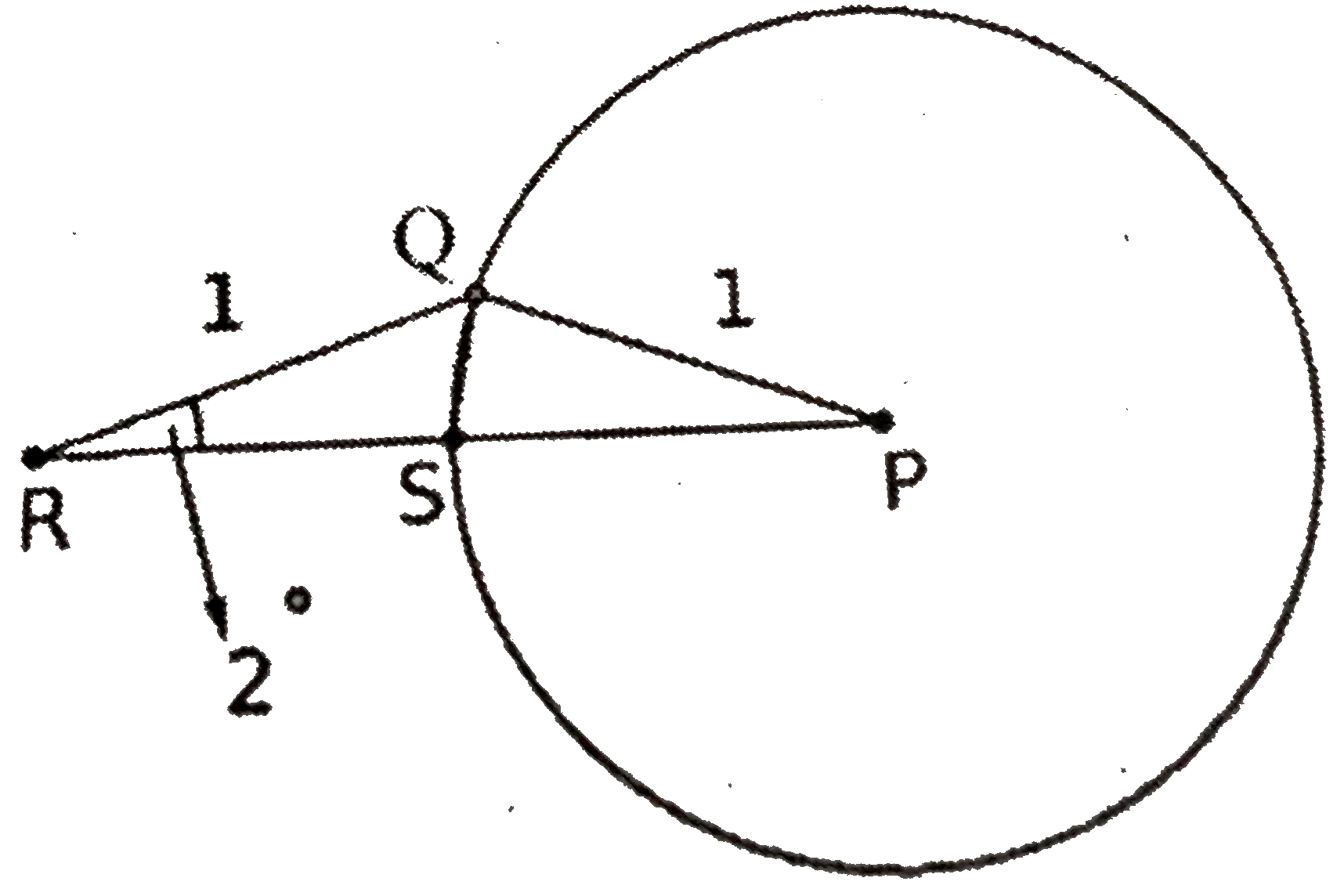 A86∘B87∘C88∘D89∘
A86∘B87∘C88∘D89∘Points P, Q and Rare on a circle such that ∠PQR=40∘and∠QRP=60∘. Then the subtended angle by arc QR at the centre is :
A80∘B120∘C140∘D160∘P is a point outside a circle with centre O, and it is 14 cm away from the centre. A secant PAB drawn from P intersects the circle at the points A and B such that PA = 10 cm and PB = 16 cm. The diameter of the Circle is:
A10 cmB13 cmC12 cmD11 cm
P and Q are two points on circle with centre O. The point R is on the minor arcPQ. The tangents from P and Q meet at S. If ∠PSQ=20∘ them ∠PRQ is-
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle . A and B are point P outside the circle . A and B are point on the circle . If ∠PAB=47∘ , then ∠OAB is equal to :
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=40∘, then ∠OABis equal to:
View SolutionPA and PB are two tangents to a circle with centre 0. from a point P outside the circle. A and B are points on the circle. If ∠APB=70∘ then ∠OAB is equal to:
View SolutionPA and PB are two tangents to a circle with centre O, from a point P outside the circle. A and B are points on the circle. If ∠APB=100∘ , then OAB is equal to:
View Solution
