If the matrix AB is zero, then It is not necessary that either A=O or, B=O (b) A=O or B=O (c) A=O and B=0 (d) all the above statements are wrong
Given : the matrix AB
is zero
Then take A=[0040] and B=[0010]
As AB=[0040][0010]
AB=[0000]
As we see here none of A and B are nul matrices.
Hence, if AB is zero it is not necessary that either A=O or B=O.
Therefore correct option is (a)
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
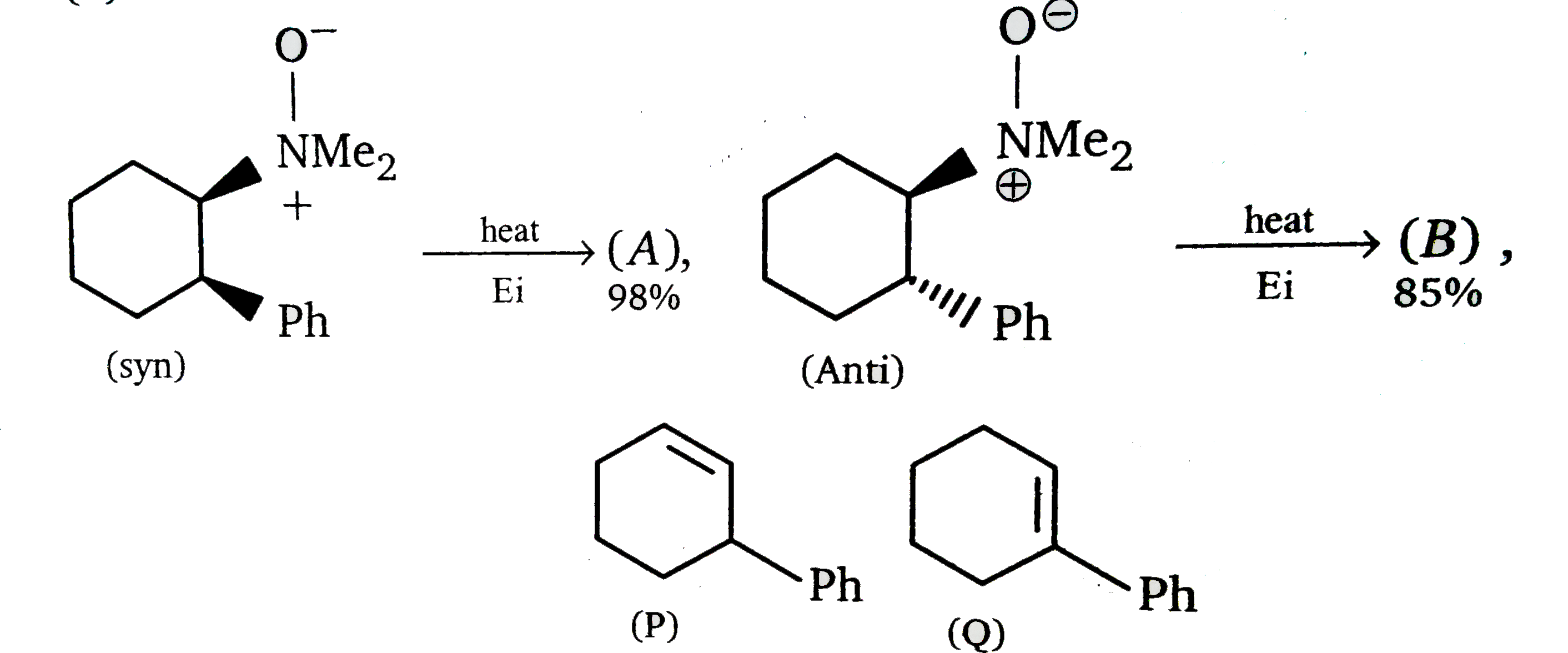
Product (A) &(B) o the above reaction is:AA=P,B=PBA=Q,B=QCA=P,B=QDA=Q,B=P - Question 2 - Select One
The abbreviation B.O.D. stands for
ABiological oxygen dificitBBiological oxygen demandCBiochemical oxygen dificitDBiological oxygen derivative - Question 3 - Select One
B.O.D is connected with
AOrganic matterBMicrobesCMicrobes and organice matterDNone of the above
Give examples of matrices A and B such that AB≠BA . (ii) A and B such that AB=O but A≠O, B≠O
View SolutionTwo fixed points A and B are taken on the coordinates axes such that OA=a and OB=b . Two variable points A' and B' are taken on the same axes such that OA′+OB′=OA+OB. Find the locus of the point of intersection of AB′ and A′B.
View SolutionShow with the help of an example that AB=O whereas BA≠O, where O is a zero matrix and A,B are both non-zero matrices.
View SolutionA point O is taken inside an equilateral four sided figure ABCD such that its distances from the angular points D and B are equal. Show that AO and OC are in one and the same straight line. GIVEN : A point O inside an equilateral quadrilateral four sided figure ABCD such that BO=OD. TO PROVE : AO and OC are in one and the same straight line.
View SolutionIf B is an idempotent matrix, and A=I−B, then a. A2=A b. A2=I c. AB=O d. BA=O
View Solution

