If V=43πr3 , at what rate in cubic units is V increasing when r=10 and drdt=0.1?
To find the rate at which the volume V is increasing when r=10 and drdt=0.1, we start with the formula for the volume of a sphere:
V=43πr3
Step 1: Differentiate V with respect to time t
To find the rate of change of volume with respect to time, we differentiate both sides of the equation with respect to t:
dVdt=ddt(43πr3)
Step 2: Apply the chain rule
Using the chain rule, we differentiate r3:
dVdt=43π⋅3r2⋅drdt
Step 3: Simplify the expression
The 3 in the numerator and denominator cancels out:
dVdt=4πr2⋅drdt
Step 4: Substitute the known values
Now, we substitute r=10 and drdt=0.1:
dVdt=4π(102)⋅0.1
Step 5: Calculate 102
Calculating 102:
102=100
Step 6: Substitute and calculate
Now substitute 100 back into the equation:
dVdt=4π⋅100⋅0.1
Step 7: Simplify further
Calculating 100⋅0.1=10:
dVdt=4π⋅10
Step 8: Final calculation
Finally, calculate 4⋅10:
dVdt=40π
Thus, the rate at which the volume V is increasing when r=10 and drdt=0.1 is:
dVdt=40π cubic units
---
Similar Questions
The radius of a circle is increasing at a rate (drdt)=α . Find the rate at which its area is increasing when radius is equal to 3 m.
View SolutionThe radius of a circle is increasing uniformly at the rate of 0.3 centimetre per second. At what rate is the area increasing when the radius is 10 cm ? (Take π=3.14)
View Solution
Knowledge Check
- Question 1 - Select One
If V=43πr3, at what rate in cubic units is V increasing when r = 10 and drdt = 0.01?
AπB4πC40πD4π/3 - Question 2 - Select One
In the formula V=13pr2h, if V=9.42 units, h=4 units and π=3.14, then r is
A94 unitsB32 unitsC23 unitsD49 units - Question 3 - Select One
dvr2=4πdr, when r=0,v=0
Av=13πr2hBv=4πr3Cv=43πr3Dv=4πr2h
A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Then the depth of the wheat is increasing at the rate of(A) 1 m3/h (B) 0.1 m3/h (C) 1.1 m3/h (D) 0.5 m3/h
View Solution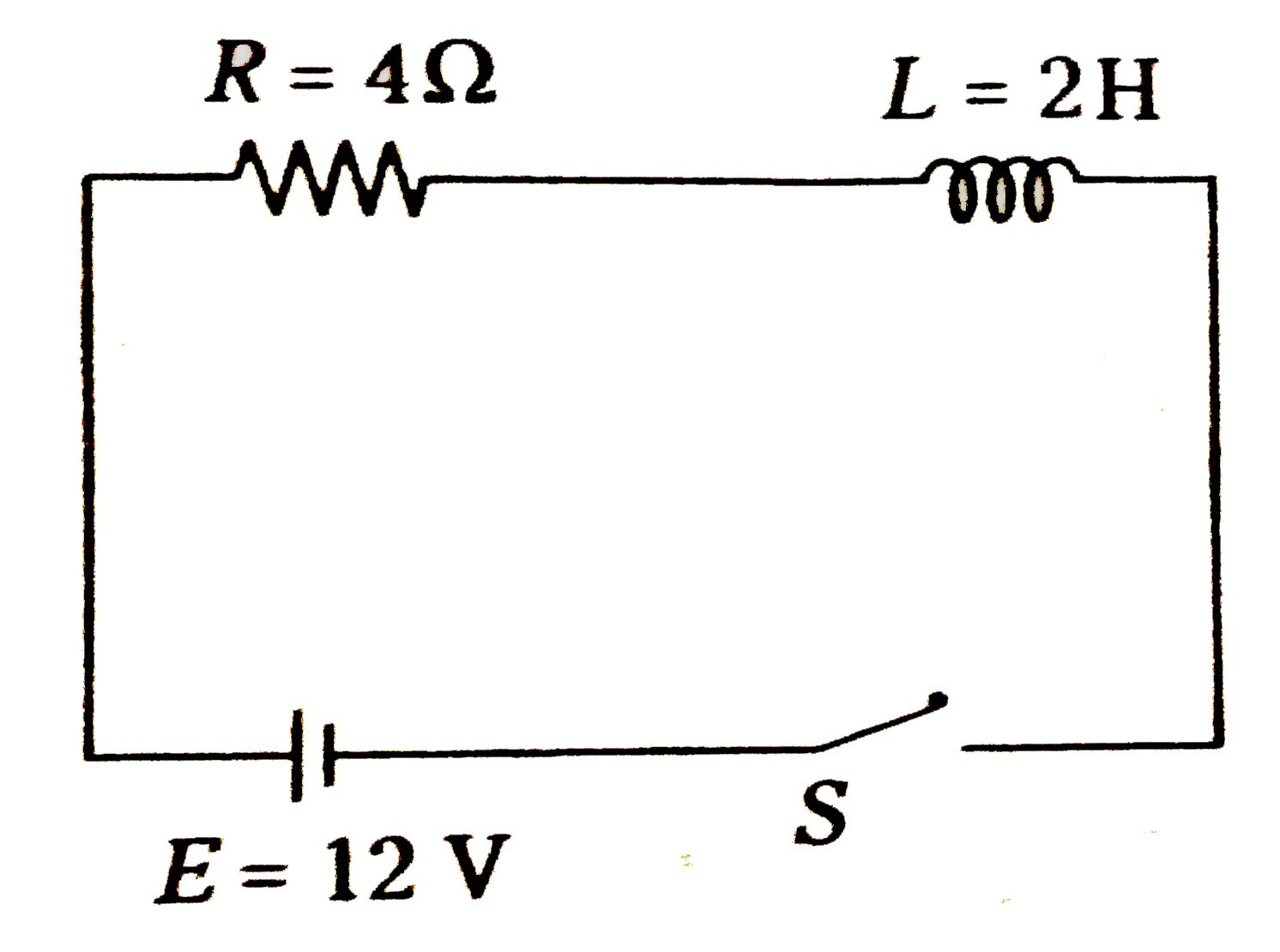
At t = 0, switch S is closed, calculate
(i) initial rate of increase of current, i.e., didtat t=0.
(ii) didt at time when current in the circuit is 0.5A.
(iii) Current at t = 0.6 s.
(iv) rate at which energy of magnetic field is increasing, rate of heat produced in resistance and rate at which energy is supplied by battery when i = 0.5 A.
(v) energy stored in inductor in steady state.View SolutionIn the circuit (Fig.) what is potential difference VB−VA (in V) when current I is 5A and is decreasing at the rate of 103As−1
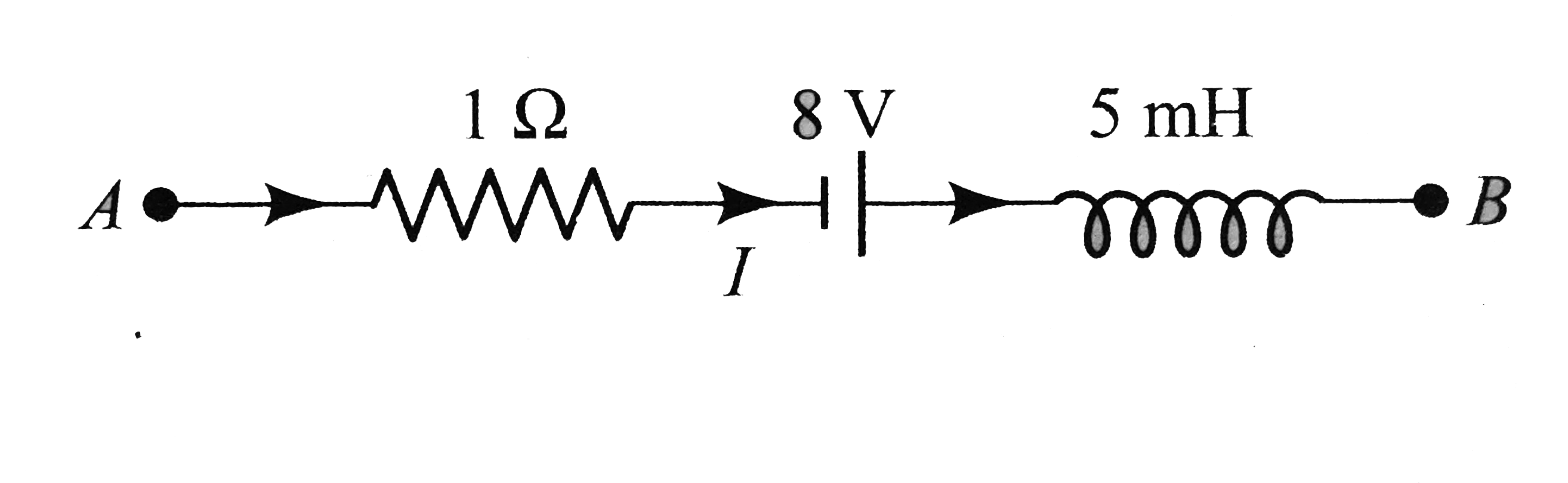 View Solution
View SolutionWhat is the potential difference VB−VA when the current i is 5A and is decreasing at a rate of 103A /s
View SolutionIf MdVdt=F−kV and V=0 what t= 0, then V is given by
View Solution

