एक कम्पनी ३ प्रकार के कैलकुलेटर A,B तथा C अपनी दो फ़ैक्टरियरों I तथा II में तैयार करती है | कम्पनी के पास A प्रकार के कण-से-कम 6,400, B प्रकार के कम-से-कम 4,000 तथा C प्रकार के कम-से-कम 4,800 कैलकुलेटरों को तैयार करने का अनुबन्ध है | फैक्टरी I में प्रतिदिन A प्रकार के 50 कैलकुलेटर, B प्रकार 50 कैलकुलेटर,B प्रकार के 50 कैलकुलेटर, और C प्रकार के 30 कैलकुलेटर तैयार होते है, जबकि फैक्टरी II में प्रतिदिन A प्रकार के 40 कैलकुलेटर, B प्रकार के 20 कैलकुलेटर और C प्रकार के 40 कैलकुलेटर तैयार होते है | फैक्टरी I को चलाने में प्रतिदिन ₹ 12,000 का खर्च आता है तथा फैक्टरी II को चलाने में ₹ 15,000 का | प्रत्येक फैक्टरी को कम-से-कम कितने-कितने दिन चलाना होगा,जिससे फैक्टरी चलाने का खर्चा न्यूनतम हो, और माँग भी पूरी हो सके | प्रश्न को रैखिक प्रोग्रामन समस्या बनाकर ग्राफ द्वारा हल कीजिए |
The correct Answer is:अतः x=80 व y=60 पर Z न्यूनतम है, Z का न्यूनतम मान 18,60,000 है | इसलिए न्यूनतम खर्च ₹ 18,60,000 है |
Topper's Solved these Questions
- रैखिक प्रोग्रामनBOOK - RAJEEV BANSALCHAPTER - रैखिक प्रोग्रामनEXERCISE - अभ्यास
13 Videos
- रैखिक प्रोग्रामनBOOK - RAJEEV BANSALCHAPTER - रैखिक प्रोग्रामनEXERCISE - अभ्यास (लघु उत्तरीय प्रश्न)
34 Videos
- यादृच्छिक चर तथा प्रायिकता बंटनBOOK - RAJEEV BANSALCHAPTER - यादृच्छिक चर तथा प्रायिकता बंटनEXERCISE - कम्पटीशन कॉर्नर
1 Videos
- रैखिक समीकरणों के निकाय का हल BOOK - RAJEEV BANSALCHAPTER - रैखिक समीकरणों के निकाय का हल EXERCISE - कम्पटीशन कॉर्नर
2 Videos
Similar Questions
निम्न व्यवरोधों के अन्तर्गत Z=20x+10y का न्यूनमीकरण कीजिए
x+2y≤40,3x+y≥30,4x+3y≥60 तथा x,y≥0
View Solutionविटामिन A और B दो विभिन्न आहार F1और F2में है |आहार F1की प्रत्येक इकाई विटामिन A की 2 इकाई तथा विटामिन B की 3 इकाई रखती है | आहार F2की प्रत्येक इकाई विटामिन A की इकाई तथा विटामिन B की 2 इकाई रखती है | आहार F1और F2की प्रत्येक इकाई की लागत क्रमशः ₹ 5 और ₹ 2.5है | किसी भी व्यक्ति के लिए एक दिवस की न्यूनतम आवश्यकता A और B की क्रमशः 40 और 50 इकाई की है | यह मानते हुए कि न्यूनतम लागत पर आहार कि आवश्यक मात्रा उपलब्ध होती है, रेखिक प्रोग्रामन का सूत्रीकरण कीजिए |
View Solutionमाना की A तथा B दो घटनाए इस प्रकार है की P¯¯¯¯¯¯¯¯¯¯A∪B=16,P¯¯¯¯¯¯¯¯¯¯A∪B=14 तथा P¯¯¯A=16 जहाँ ¯¯¯A घटना A की सम्पूरक घटना है तो घटनाए A तथा B है |
View Solutionवास्तविक संख्या α के लिए यदि रैखिक समीकरण निकाय
⎡⎢⎣1αα2α1αα2α1⎤⎥⎦⎡⎢⎣xyz⎤⎥⎦=⎡⎢⎣1−11⎤⎥⎦ के अनन्त हल है, तब 1+α+α2=.......
View Solutionएक कम्पनी दो प्रकार के टेलीफ़ोन A व B बनाती है|A प्रकार के टेलीफ़ोन बनाने में 2 घण्टे एवं 300 टेलीफोनों को एक दिन में पैक किया जा सकता है| A प्रकार के टेलीफ़ोन का विक्रय मूल्य रु 300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य रु 400 है| अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफ़ोन का निर्माण करती है तो रेखीय प्रतिबन्ध (x≥0,y≥0 के अलावा ) है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न के रेखीय कार्य योजना का सम्भाव्य क्षेत्र के निम्न प्रकार का है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त क्षेत्र के शीर्ष है:
View Solutionएक कम्पनी दो प्रकार के टेलीफोन A व B बनाती है | A प्रकार के टेलीफ़ोन बनाने में 2 घंटे एवं B प्रकार के टेलीफ़ोन बनाने में 4 घंटे लगते हैं |कम्पनी के पास 800 घंटे कार्य उपलब्ध है| 300 टेलीफोनों को एक दिन में पैक किया जाता है | A प्रकार के टेलीफोन का विक्रय मूल्य ₹300 तथा B प्रकार के टेलीफ़ोन का विक्रय मूल्य ₹400 है | अधिकतम लाभ के लिए कम्पनी A प्रकार के x तथा B प्रकार के y टेलीफोन का निर्माण करती है तो रेखीय प्रतिबंध के (x≥0,y≥0 अलावा ) है :
उपयुक्त प्रश्न का अनुकूलतम है निम्नलिखित शीर्ष पर है|
View Solutionनिचे दिये गये ग्राफ में दो प्रकार के वाहनों A व B के छ वर्षो के प्रदूषण का आंकड़ा दिया गया है ।A घरेलू वाहनों तथा B व्यावसायिक वाहनों को दर्शाता है ,तो ग्राफ का अध्ययन क्र आगे दिये गये प्रशनो के उत्तर दीजिए|
दिये गये वर्षो में से कितने वर्षो में B का प्रदूषण A के प्रदूषण से कम रहा है ?
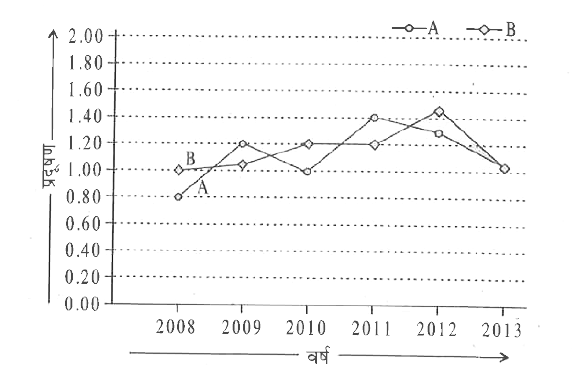
View Solutionनिचे दिये गये ग्राफ में दो प्रकार के वाहनों A व B के छ वर्षो के प्रदूषण का आंकड़ा दिया गया है ।A घरेलू वाहनों तथा B व्यावसायिक वाहनों को दर्शाता है ,तो ग्राफ का अध्ययन क्र आगे दिये गये प्रशनो के उत्तर दीजिए|
दिये गये वर्षो में से कितने वर्षो में B का प्रदूषण A के प्रदूषण से कम रहा है ?

View Solutionरोगों के प्रकार तथा कारण
View Solutionतना तथा तने के प्रकार
View Solutionमिश्रण तथा विलियन के प्रकार
View Solutionजनन तथा जनन के प्रकार
View Solutionबल का परिचय तथा बल के प्रकार
View Solutionवर्गीकृत आंकड़ों की 'से कम प्रकार' और 'से अधिक प्रकर' की संचयी बारम्बारता वक्रों के प्रतिच्छेद बिन्दु के 'भुज' से प्राप्त होता है आंकड़ों का----
View Solution
