As shown in the figure, initially both th springs are in normal length (L0). At t=0, the block is given a rightward velocity v0=2m/s. The mass of the block is (14/3)kg. How much distance does th block cover before it comes to rest for the first time? (The spring constant of the left spring is K0=2N/m and that of the right spring is not constant and varies as k=k0x, where x is the compression in the spring)
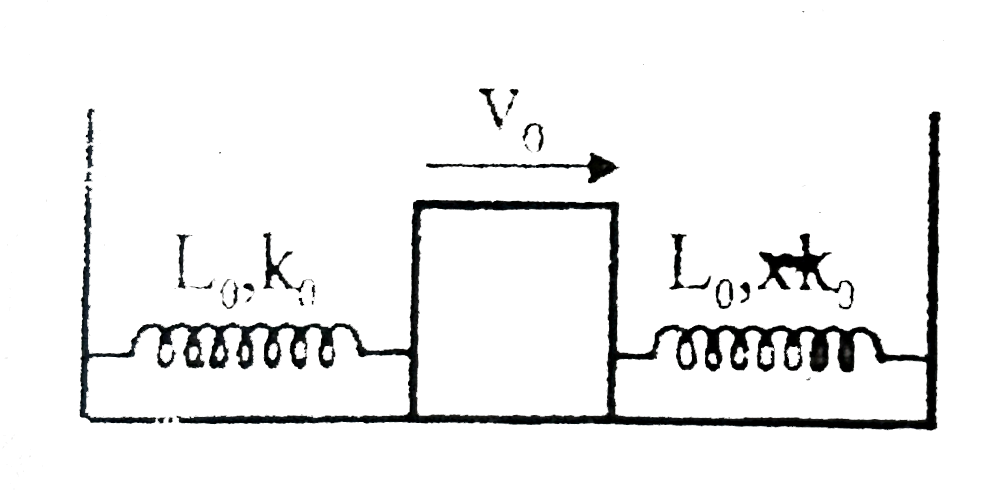
2m
4m
6m
8m
The correct Answer is:A
12mv20=12K0(23x2+x2)
⇒12(143)(2)2=12×2×(23x3+x2)
⇒2x3+3x2−28=0
⇒2x2(x−2)+7x(x−2)+14(x−2)=0
⇒x=2m
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - part-2 physics
63 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A 16kg block moving on a frictionless horizontal surface with a velocity of 4m/s compresses an ideal spring and comes to rest. If the force constant of the spring be 100N/m, then how much is the spring commpressed ?
View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0A block of mass m is placed on a smooth block of mass M=m with the help of a spring as shown in the figure. A velocity v0 is given to upper block when spring is in natural length. Find maximum compression in the spring.
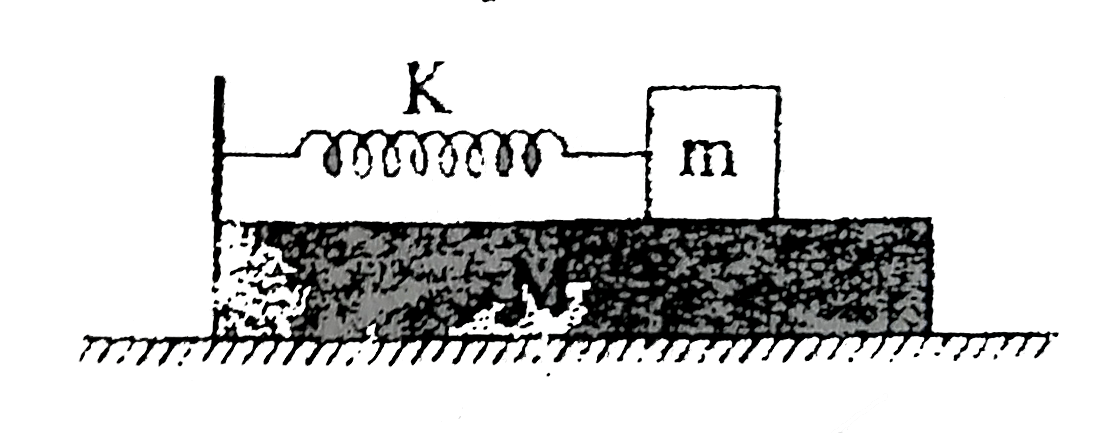 A√m2KV0B√mKv0C√2mKv0D2√mKv0
A√m2KV0B√mKv0C√2mKv0D2√mKv0A block of mass 'm' is attached to a spring in natural length of spring constant 'k'. The other end A of the spring is moved with a constat velocity v away from the block . Find the maximum extension in the spring.
 A14√mv2kB√mv2kC12√mv2kD2√mv2k
A14√mv2kB√mv2kC12√mv2kD2√mv2k
A block of mass 4 kg is released from the top of an inclined smooth surface as shown in figure If spring constant of spring is 100M/m and block comes to rest after compressiong spring by 1 m, find the distance travelled by the block before it comes t o rest.

View SolutionA block of mass √2 kg is released from the top of an inclined smooth surface as shown in fighre. If spring constant of spring is 100 N/m and block comes to rest after compressing the spring by 1 m, then the distance travelled by block befor it comes to rest is

View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionBlock of mass 2m is given v0 towards the right. If L is the natural length of spring constant k, find the maximum elongation of the spring.

View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View Solution
