A drum major's baton consists of two masses $m_{1}$ and $m_{2}$ separated by a thin rod length l. The baton is thrown into the air. The problem is to find the baton's center of mass and the equation of motion for the center of mass.

Video Solution

Text Solution

Verified by Experts

Let the position vectors of $m_{1}$ and $m_{2}$ be $r_{1}$ and $r_{2}$ .
The position vector of the center of mass, measured from the same origin, is
$R = \frac{m_{1} r_{1} + m_{2} r_{2}}{m_{1}} + m_{2}$
where we have neglected the mass of the thin rod. The center of mass lies on the line joining $m_{1}$ and $m_{2}$ . To show this, suppose first that the tip of R dows not lie on the line, and consider the vectors $r_{1} r_{2}$ from the tip of R to $m_{1}$ and $m_{2}$
From the sketch we see that $r_{1} = r_{1} - R$
$r_{2} = r_{2} - R$
Using equation (1) gives $r_{1} = r_{1} - \frac{m_{1} r_{1}}{m_{1} + m_{2}} - \frac{m_{2} r_{2}}{m_{1} + m_{2}} = \frac{m_{2}}{m_{1} + m_{2}} (r_{1} - r_{2})$
$r_{2} = r_{2} - \frac{m_{1} r_{1}}{m_{1} + m_{2}} - \frac{m_{2} r_{2}}{m_{1} + m_{2}} = - (\frac{m_{1}}{m_{1} + m_{2}}) (r_{1} - r_{2})$
$r_{1}$ and $r_{2}$ are propotional to $r_{1} - r_{2}$ , the vector from $m_{1}$ to $m_{2}$ . Hence $r_{1}$ and $r_{2}$ lie along the line jpining $m_{1}$ and $m_{2}$ as shown.

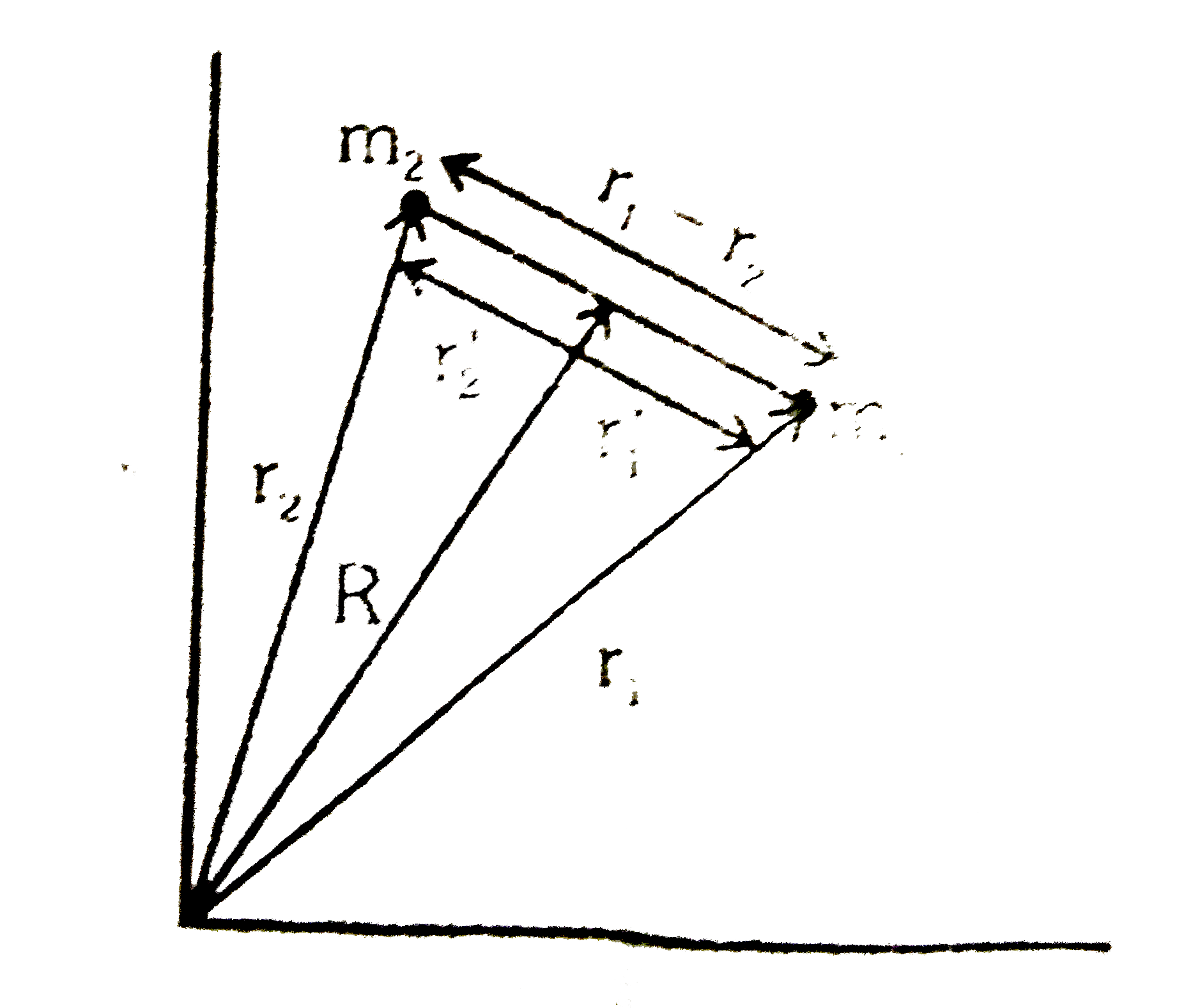
Furthermore, $r_{1} = \frac{m_{2}}{m_{1} + m_{2}} (r_{1} - r_{2}) = \frac{m_{2}}{m_{1} + m_{2}}$
$r_{2} = \frac{m_{1}}{m_{1} + m_{2}} (r_{1} - r_{2}) = \frac{m_{1}}{m_{1} + m_{2}} l$
Assuming that friction is negligible, the external force on the baton is $F = m_{1} g + m_{2} g$
The equation of motion of the center of mass is $(m_{1} + m_{2}) R = (m_{1} + m_{2}) g$ or $R = g$
The center of mass follows the parabolic trajectory of single mass in a uniform gravitational field.

Updated on:21/07/2023