Mass center of truncated boldes
A truncated body is made by removing a portion of a body. Find mass center of the following truncated disk made by removing disk of radius equal to half of the original disk as shown in the figure. Radius of the original uniform disk is r.

To find mass center of truncated bodies we can make use of superposition principle that is. If we add the removed portion in the same place we obtain the original body. The idea is illustrated in the following figure.

The removed portion is added to the trucated body keeping their location unchanged relative to the coordinate frame.
Denoting massses of the truncated body, removed portion and the original body by mtb,mrp and mob and location of their mass centres by xtb,xrp and xob, we can write mtbxtb+mrbxrp=mobxob
From the above equation we obtain position coordinate xtb of the mass center of the truncated body.
xtb=mobxob−mrbxrpmtb
Denoting mass per unit area by sigma, we can express the masses mtb,mrp and mob.
Mass of truncated body mtb=σ{π(r2−r24)}=3σπr24
Mass of the removed portion mrp=σπr24
Mass of the original body mob=σπr2
Mass center of the truncated body xtb
Mass center of the removed portion xrp=r2
Mass center of the original body xob=0
Substituting the above values in equation (1), we obtain the mass the center of the truncated body.
xtb=mobxob−mrbxrpmtb=(σπr2)×0−(σπr24)(r2)3σπr24=−r6
Mass center of the truncated body is at point (−r6,0)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Mass center of composite bodies
A composite body is made of joining two or more bodies. Find mass center of the following composite body made by joining a uniform disk of radius r and a uniform square plate of the same mass per unit area.
View SolutionFind coordinates of mass center of a quarter sector of a uniform disk of radius r placed in the first quadrant ofa Cartesian coordinate system with centre at origin.
View Solution
Knowledge Check
Find the position of center of mass of the uniform lamina shown in figure, if small disc of radius a2 is cut from disc of radius a.
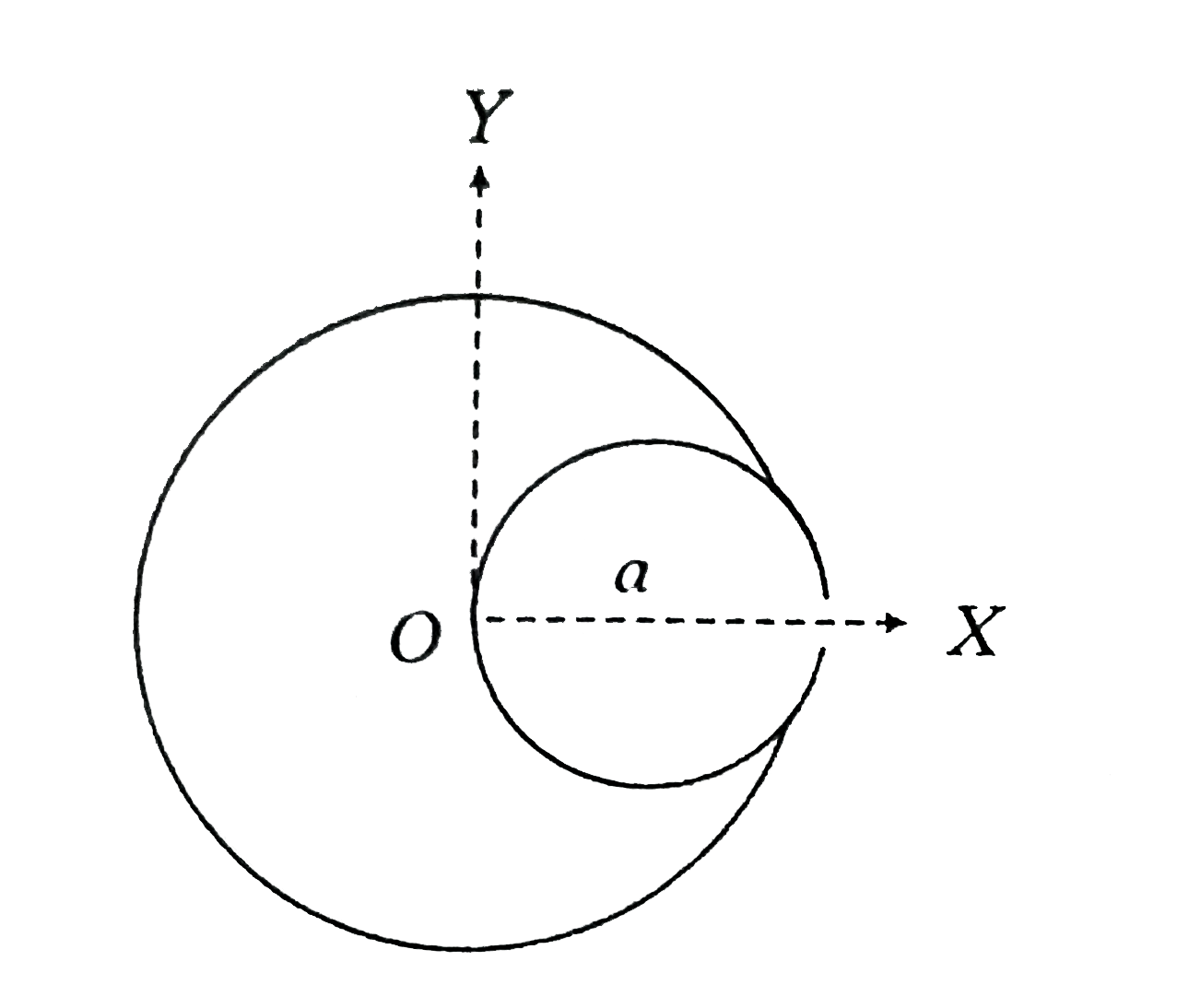 A(−a6,a)B(−a2,0)C(−a6,0)D(−a3,0)
A(−a6,a)B(−a2,0)C(−a6,0)D(−a3,0)Center of mass of two thin uniform rods of same length but made up of different materials. & kept as shown, can be, if the meeting point is the origin of co-ordinated
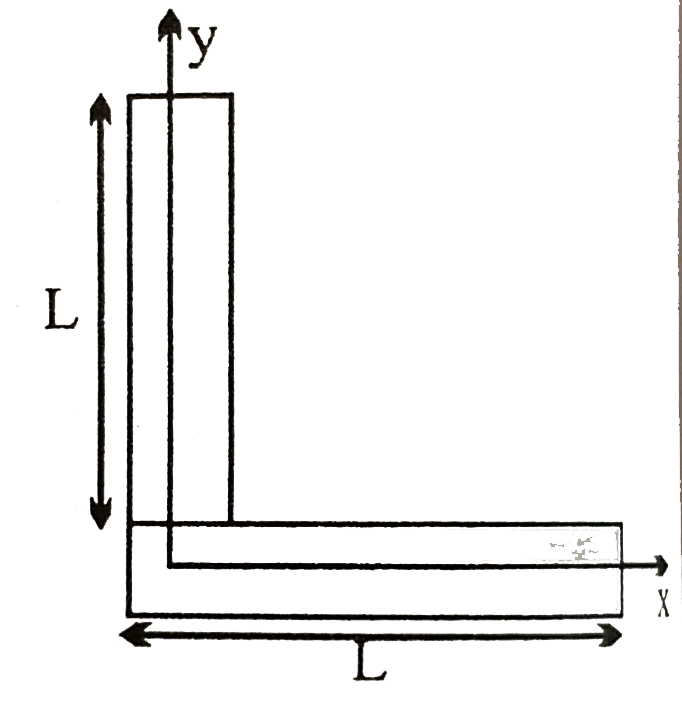 A(L/2,L/2)B(2L/3,L/2)C(L/3,L/3)D(L/3,L/6)
A(L/2,L/2)B(2L/3,L/2)C(L/3,L/3)D(L/3,L/6)Find the coordinates of centre of mass of a uniform semicircular closed wire frame with respect to the origin which is at its centre. Radius of the circular portion is R
 A(4R3π,0)B(2Rπ+2,0)C(2Rπ,0)D(Rπ+2,0)
A(4R3π,0)B(2Rπ+2,0)C(2Rπ,0)D(Rπ+2,0)
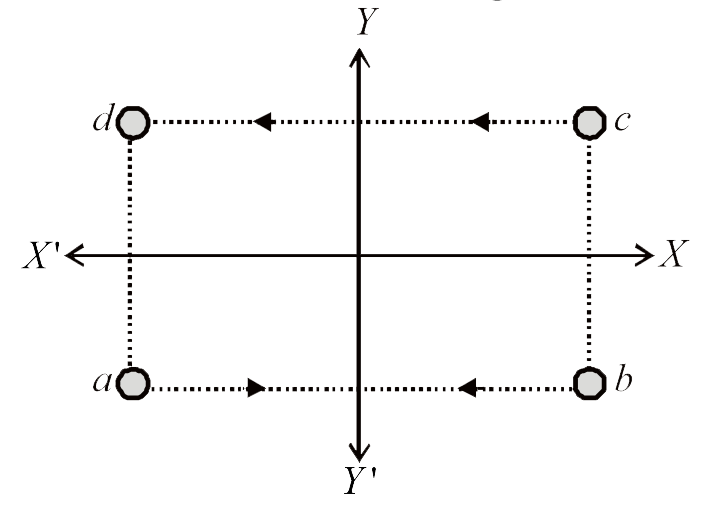
Four bodies of equal mass start moving with same speed as shown in the figure. In which of the following combination the centre of mass will remain at origin
View SolutionFind coordinates of mass center of a uniform semicircular plate of radius r placed symmetric to the y-axis of a Cartesian coordinate system, with centre at origin.
View SolutionFind coordinates of mass center of a quarter ring of radius r placed in the first quadrant of a Cartesian coordinate system, with centre at origin.
View SolutionFigure shows a composite body made up by welding a thin rod (of mass m and length r) normally at the centre P of a thin semicircular disc (of mass m and radius r). What are corrdinates of centre of mass of the system ?

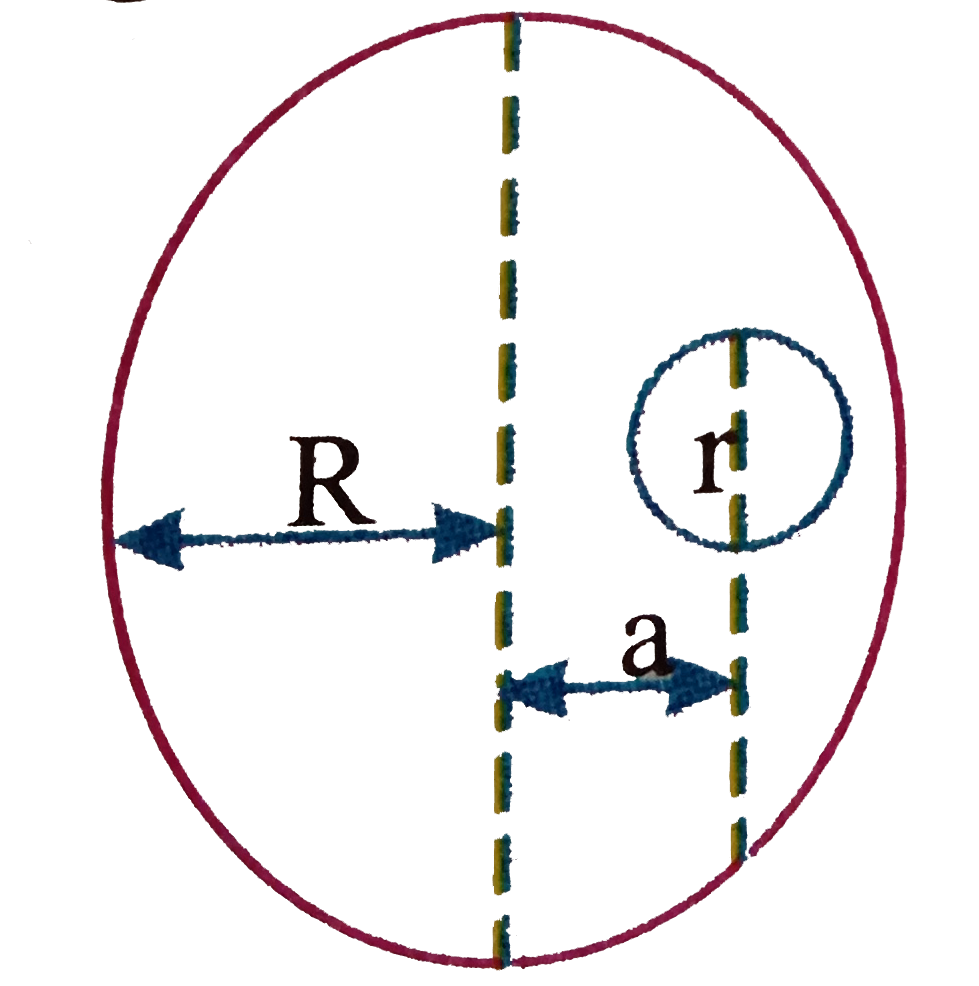
View SolutionA circular hole of radius r is made in a disk of radius R and of uniform thickness at a distance a from the centre of the disk. The distance of the new centre of mass from the original centre of mass is
View Solution
