A disk sliding with velocity u on a smooth horizontal plane strikes another identical disk kept at rest as shown in the figure. If the impact between the disks is perfectly elastic impact, find velocities of the disks after the impact.
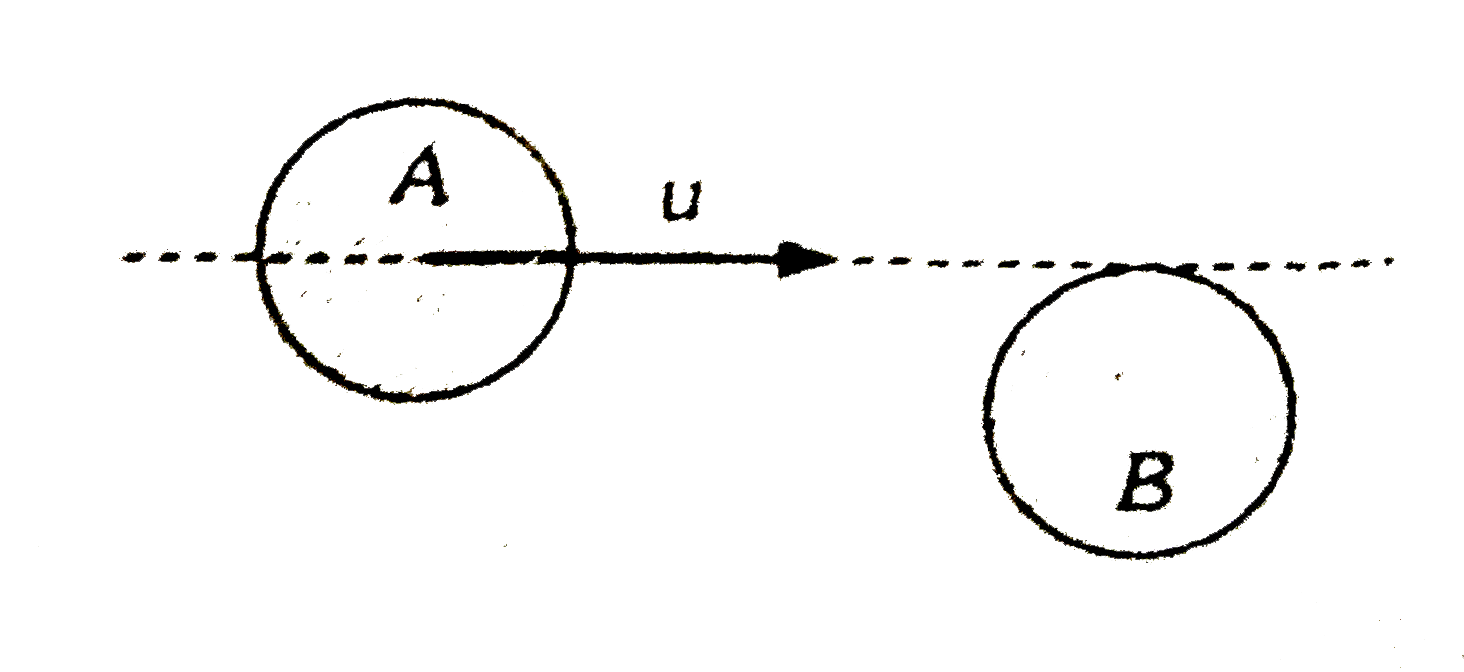
We first show velocity components along the t and the n-axis immediately before and after the impact. Angle that the line of impact makes with velocity u is 30∘

Component along t-axis Components of momentum along the t-axis of each disk, considered separately, is conserved. Hence, t-component of velocities of each of the bodies remains unchanged.
vAt=uAt=u2 and vBt=uBt=0 ...(i)
The component along the n-axis of the total momentum of the two bodies is conserved
mBvBn+mAvAn=mBuBn+mAuAn→mvBn+mvAn=m×0+mu√32
vBn+vAn=u√32 ...(ii)
Concept of coefficient of restitution e is applicable only for the n-component velocities.
vBn−VAn=e(uAn−UBn)→ vBn−VAn=u√32 ...(iii)
From equations (ii) and (iii), we have vAn=0 and vBn=u√32 ...(iv)
From equations (i) and(iv) we can write velocities of both the disks.
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions

A rod of length l forming an angle θ with the horizontal strikes a frictionless floor at A with its centre of mass velocity v0 and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.
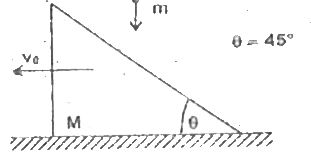
View SolutionA triangular wedge of mass M is moving with uniform velocity v0 along a smooth horizontal surface in the leftward direction. A particle of mass m falls from rest from height h onto the inclined face, colliding elastically with it. Find velocity of the ball and wedge after the impact taking M = 2m.
View Solution
Knowledge Check
A ping-pong ball strikes a wall with a velocity of 10ms−1. If the collision is perfectly elastic, find the velocity if ball after impact
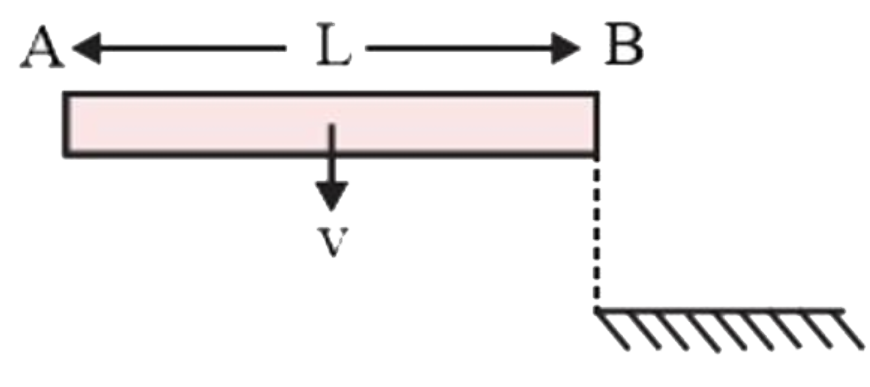
A−20ms−1B−5ms−1C1.0ms−1D−10ms−1A rod AB of length L and mass M is free to move on a frictionless horizontal surface. It is moving with a velocity v, as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact, the angular velocity of the rod AB, just after impact, is
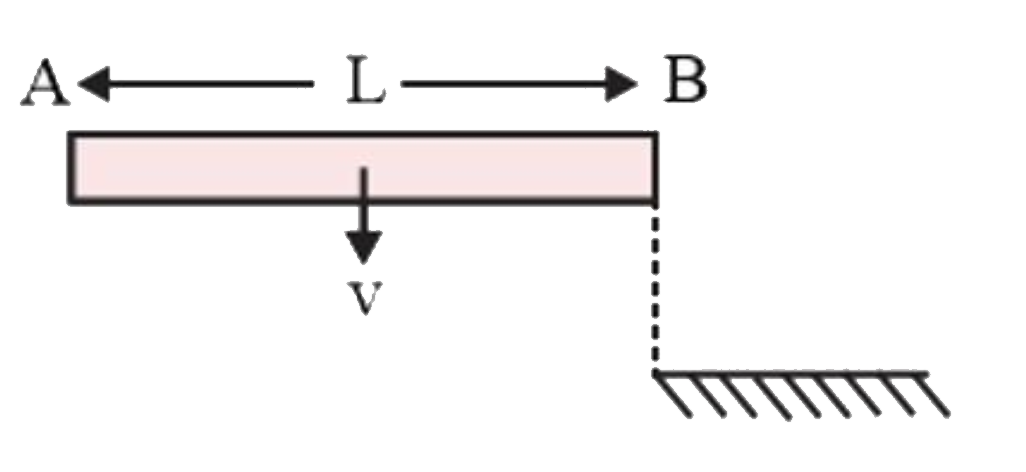 Av2LB3vLC3v2LDvL
Av2LB3vLC3v2LDvLA ball of mass m moving with velocity v, collide with the wall elastically as shown in the figure. After impact the change in angular momentum about P is :
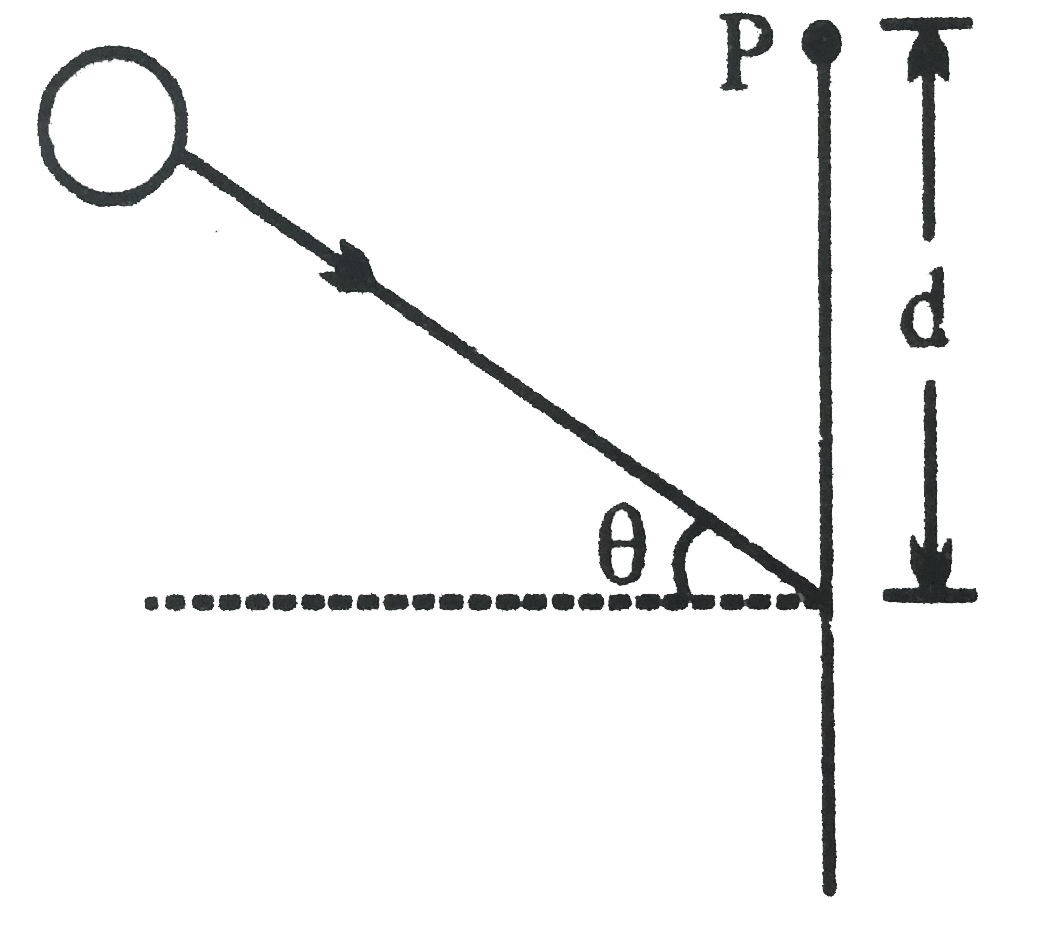 .A2mvdB2mvdcosθC2mvdsinθDzero
.A2mvdB2mvdcosθC2mvdsinθDzero
A ball of mass m moving with velocity u impinges on a ball of mass em moving with velocity eu in the opposite direction. If the impact be direct and e be the coefficient of restitution then the velocity of the second ball after impact is the same as that of the first ball before impact.
View SolutionA rod AB of length L and mass M is free to move on a frictionless horizontal surface . It is moving with a velocity v , as shown in figure. End B of rod AB strikes the end of the wall. Assuming elastic impact , the angular velocity of the rod AB , just after
View Solution
A rod of length l forming an angle θ with the horizontal strikes a frictionless floor at A with its centre of mass velocity v0 and no angular velocity. Assuming that the impact at A is perfectly elastic. Find the angular velocity of the rod immediately after the impact.
View SolutionA particle at rest is constrained to move on a smooth horizontal surface. Another identical particle hits the fractional particle with a velocity v at an angle θ=60∘ with horizontal. If the particles move together, the velocity of the combination just after impact is equal to
View SolutionA particle at rest is constrained to move on a smooth horizontal surface. Another identical particle hits the stationary particle with a velocity v at an angle θ=60∘ with horizontal. If the particles move together, the velocity of the combination just after the impact is equal to
View Solution
