The magnitude of acceleration of centre of mass of the system is

4m/s
10ms2
5ms2
2√2ms2
The correct Answer is:(D)
a=Net force on systemtotal mass of system=5g−μ(5g)5+5=50(1−0.2)10=4ms2acm=∣∣∣m1→a1+m2→a2m1+m2∣∣∣=a√2=2√2m/s
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
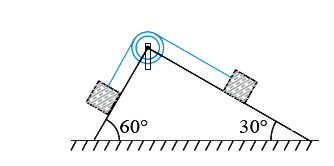
Two blocks A and B of equal masses are attached to a string passing over a smooth pulley fixed to a wedge as shown in figure. Find the magnitude of acceleration of centre of mass of the two blocks when they are released from rest. Neglect friction.

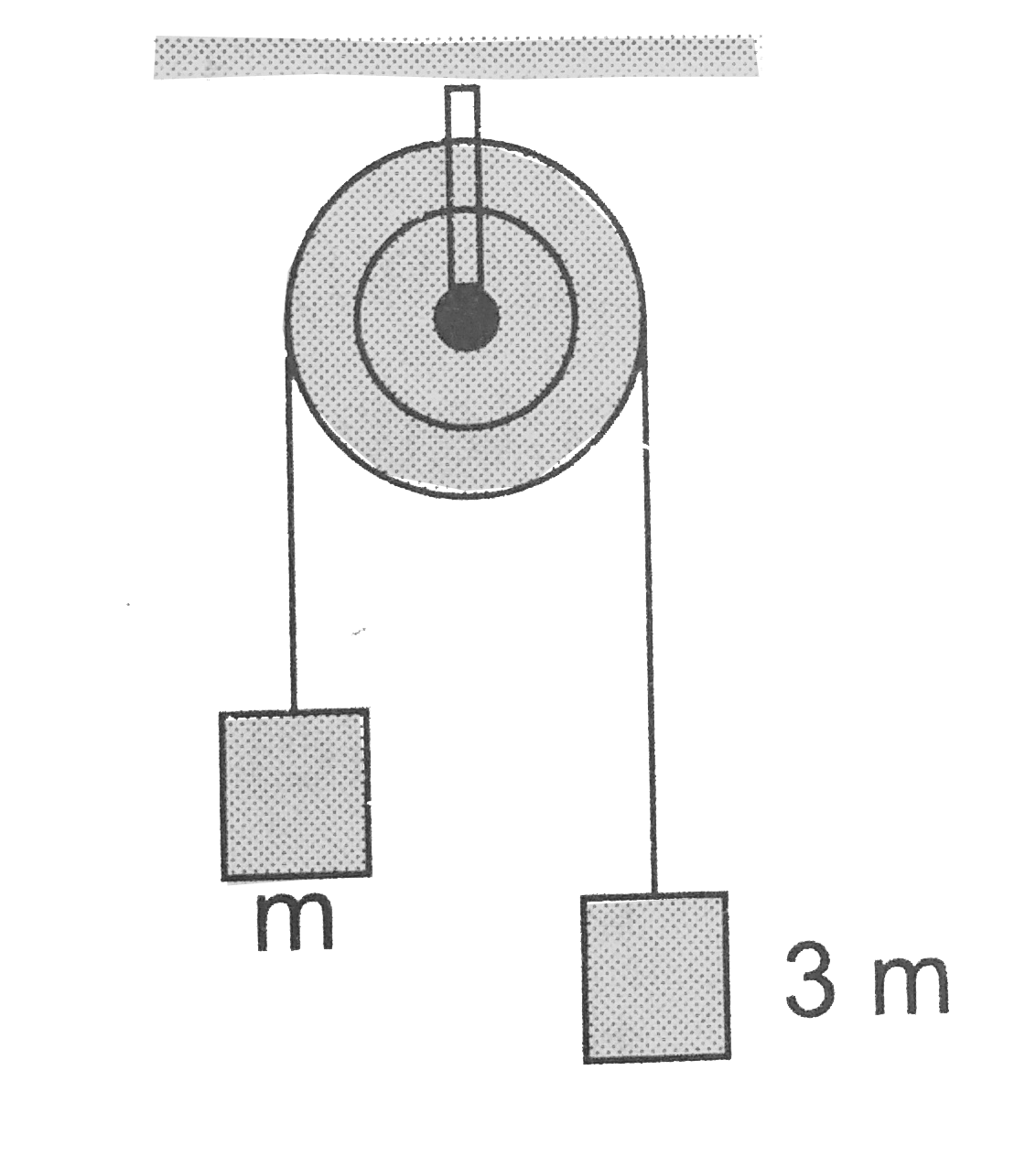
View SolutionTwo blocks of equal mass are tied with a light string, which passes over a massless pulley as shown in figure. The magnitude of acceleration of centre of mass of both the blocks is : (neglect friction everywhere)
View Solution
Knowledge Check
If the system is released, then the acceleration of the centre of mass of the system is :
 .Ag4Bg2CgD2 g
.Ag4Bg2CgD2 gIn a system of particles 8kg mass is subjected to a force of 16N along + ve x-axis and another 8kg mass is subjected to a force of 8N along + ve y-axis. The magnitude of acceleration of centre of mass and the angle made by it with x-axis are given, respectively, by
A√52ms2,θ=45∘B3√5ms2,θ=tan−1(23)C√52ms2,θ=tan−1(12)D1ms2,θ=tan−1√3In a system of particles 8kg mass is subjected to a force of 16N along +ve x-axis and another 8kg is subjected to a force of 8N along +ve y-axis. The magnitude of acceleration of centre of mass and the angle made by it with x-axis are given respectively by :
A√52ms−2,θ=45∘B3√5ms−2,θ=tan−1(2/3)C√52ms−2,θ=tan−1(1/2)D1ms−2,θ=tan−1√3
Calculate centre of mass of the system
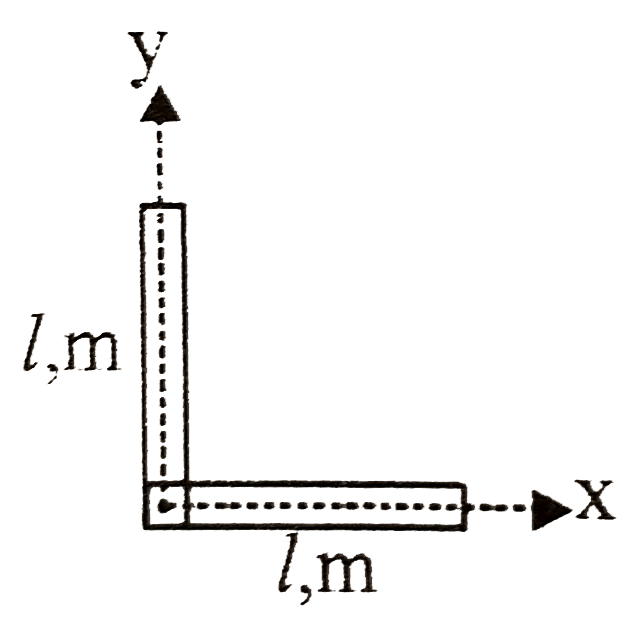
View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View SolutionTwo particles having mass ratio n:1 are interconnected by a light inextensible string that passes over a smooth pulley . If the system is released , then the acceleration of the centre of mass of the system is
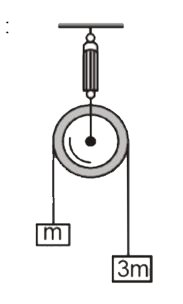
View SolutionIf the system is released, then the acceleration of the centre of mass of the system :
View Solution(1) Find the acceleration of centre of mass of the system shown.
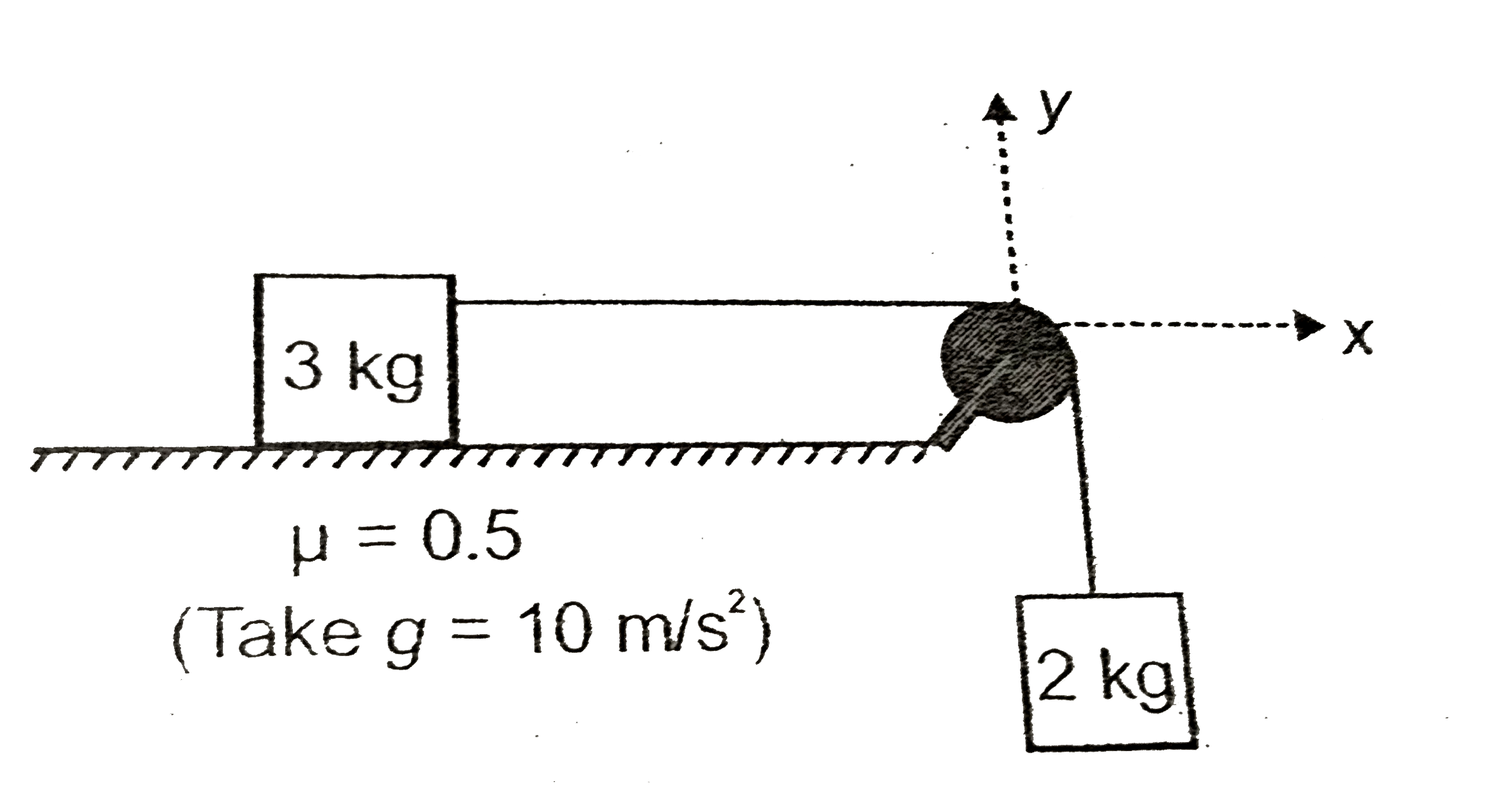
(ii) Find the normal reaction applied by the pulley on the thread.
View Solution
