For shown situation find the maximum elongation in the spring. Neglect friction everywhere. Initiallthe blocks are at rest and spring is unstreched.

4F3K
3F4K
4FK
2FK
The correct Answer is:(A)
By using reduced mass concept this system can be reduced to 
Where μ=(3m)(6m)3m+6m=2m and F1= Force on either block w.r.t. centre of mass of the system
=F2+(3m)acm=F2+(3m)(F−F/29m)=F2+F6=23F
Now from wrok energy theorm, 2F3xm=12Kx2m⇒xm=4F3K
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionIn the situations shown in the figure surfaces are frictionless. Find the maximum extension of the springs if blocks are initially at rest and springs are initially in natural lengths.

View Solution
Knowledge Check
In the previous problem , the maximum elongation of the spring is
A2cmB3cmC2√3cmD2√5cmFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.
 AmgBmg/2C3mg/2D2 mg
AmgBmg/2C3mg/2D2 mgA block ofmass m is attached with a spring in its natural length, of spring constant k. The other end A of spring is moved with a constant acceleration 'a' away from the block as shown in the figure−3.74. Find the maximum extension in the spring. Assume that initially block and spring is at rest w.r.t ground frame:
 AmakB12makC2makD124mak
AmakB12makC2makD124mak
Two blocks of mass 10 kg and 2 kg are connected by an ideal spring of spring constant 1000 N/m and the system is placed on a horizontal surface as shown. The coefficient of friction between 10 kg block and surface is 0.5 but friction is assumed to be absent between 2 kg and surface. Initially blocks are at rest and spring is unstretched then 2 kg block is displaced by 1 cm to elongate the spring then released. Then the graph representing magnitude of frictional force on 10 kg block and time t is : (Time t is measured from that instant when 2 kg block is released to move)
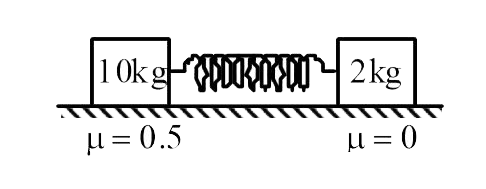
View SolutionTwo blocks of mass 10 kg and 2 kg are connected by an ideal spring of spring constant K=800N/m and the system is placed on a horizontal surface as shown.
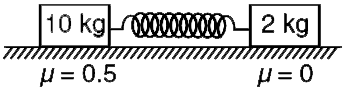
The coefficient of friction between 10 kg block and surface is 0.5 but friction is absent between 2 kg and the surface. Initially blocks are at rest and spring is relaxed. The 2 kg block is displaced to elongate the spring by 1 cm and is then released. (a) Will 10 kg block move subsequently? (b) Draw a graph representing variation of magnitude of frictional force on 10 kg block with time. Time t is measured from that instant when 2 kg block is released to move.
View SolutionIn figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
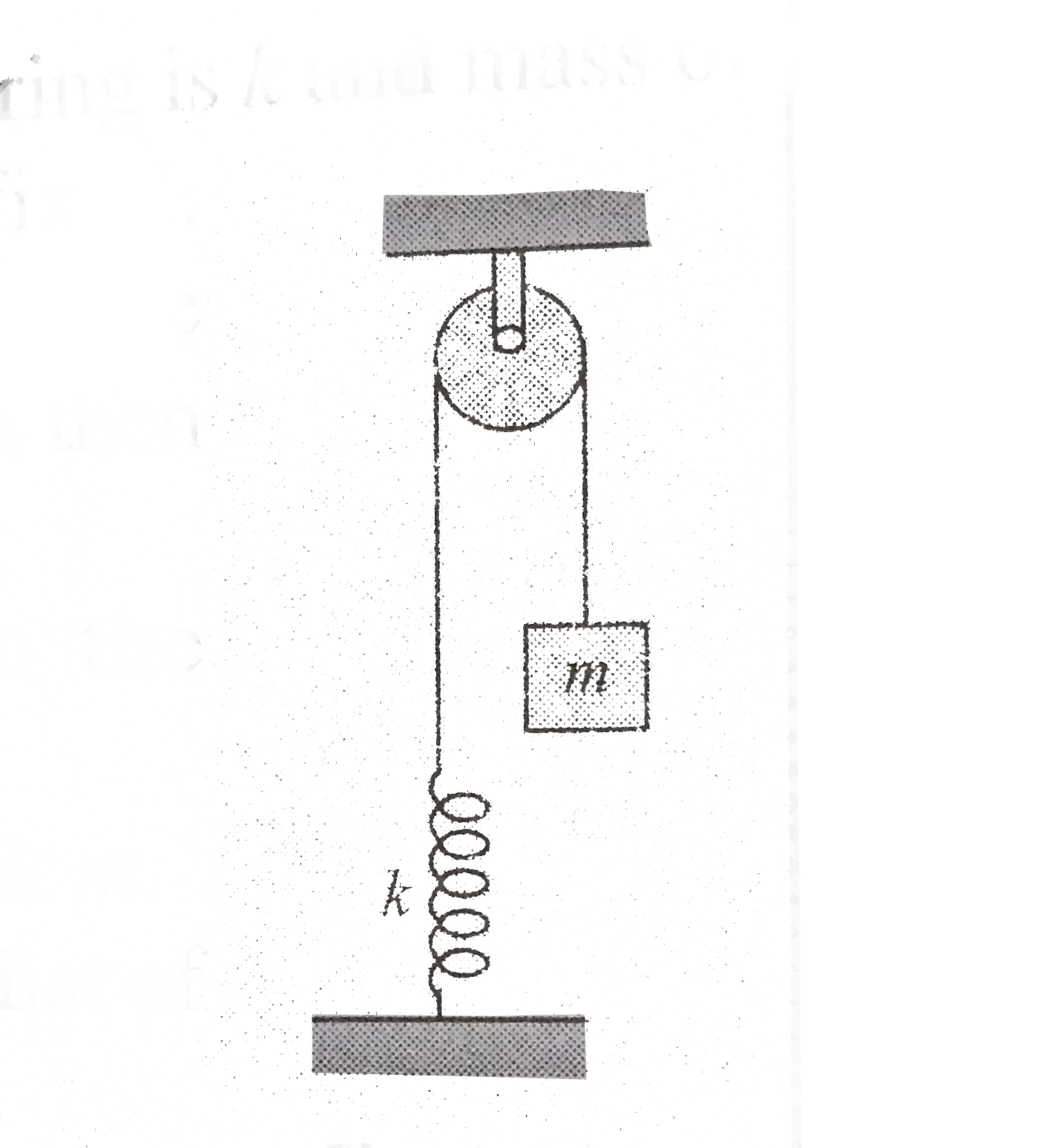
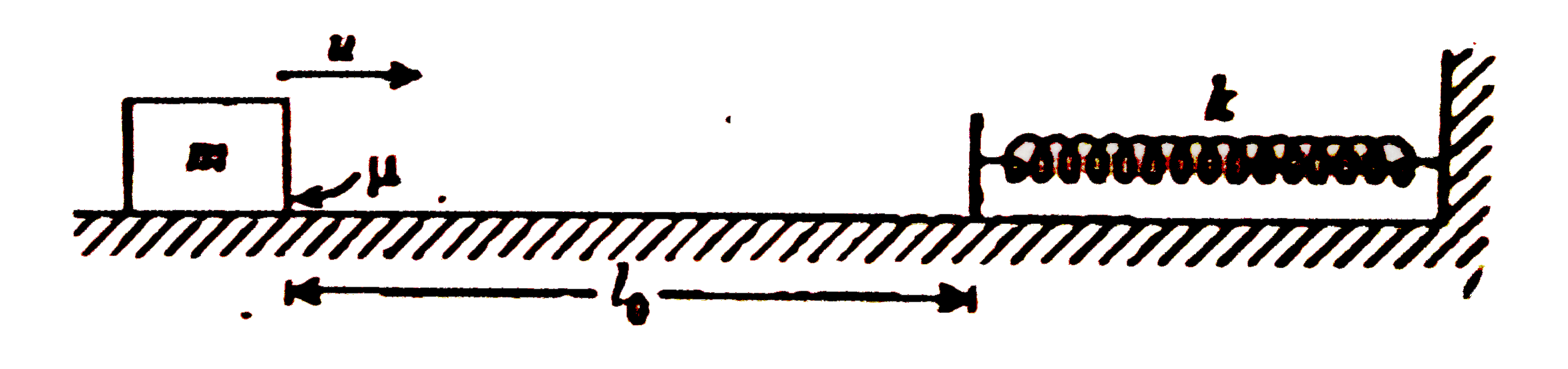
View SolutionFigure. shows a rough horizontal plane which ends in a vertical wall, to which a spring is connected, having a force constant k. Initially spring is in its relaxed state. A block of mass m starts with an initial velocity u towards the spring from a distance l0 from the end of spring shown. When block strikes at the end ofthe spring, it compresses the spring and comes to rest. Find the maximum compression in the spring. The friction coefficient between the block and the floor is μ..
View SolutionA spring, placed horizontally on a rough surface is compressed by a block of mass m, placed on the same surface so as to store maximum energy in the spring. If the coefficient of friction between the block and the surface is μ, the potential energy stored in the spring is
View Solution
