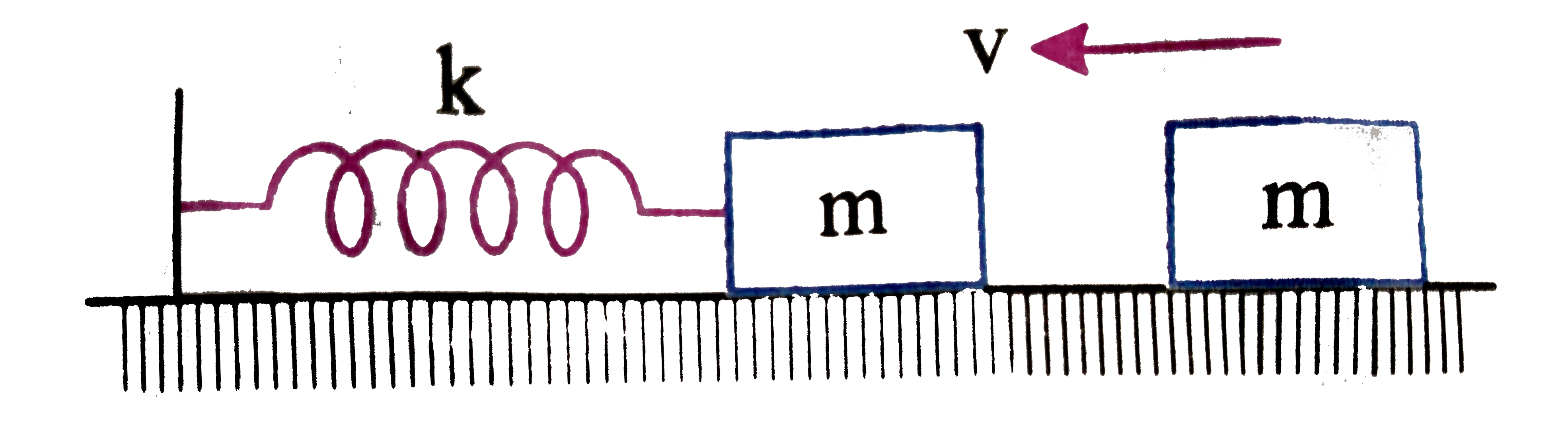
For shown situation, if collision between block A and B is perfectly elastic, then find the maximum energy stored in spring in joules.
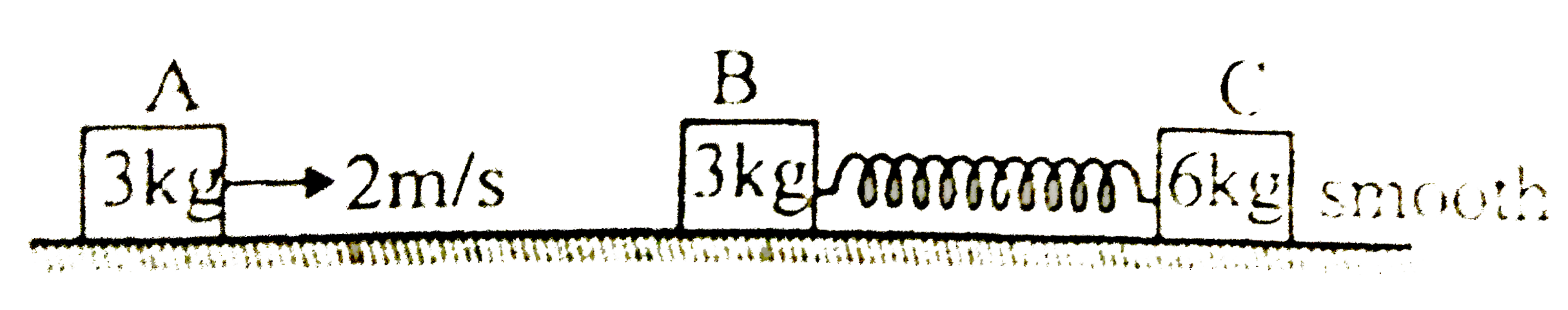
The correct Answer is:4J
At maximum compression of spring, velocities of block B and C are same (say v0 )
then by conservation of linear momentum 3(2)=(3+6)v0⇒v0=23m/s
At this instant energy stored in spring =12(3)(2)2−12(3+6)(23)2=6−2=4J
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I40videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II43videos
CENTRE OF MASS
- BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
For the shown situation, if collision between block A and B is perfectly elastic, then find the maximum energy (in joules) stored in the spring.
'(##CEN_KSR_PHY_JEE_C08_E01_031_Q20##)'View SolutionA block having mass m and charge Q is resting on a frictionless plane at a distance d from fixed large non-conducting infinite sheet of uniform charge density −σ as shown in Figure. Assuming that collision of the block with the sheet is perfectly elastic, find the time period of oscillatory motion of the block. Is it SHM ?
View Solution
Knowledge Check
- Question 1 - Select One
Rod can rotate about hinge point 'P'. A ball of mass 'm' is projected with a velocity 5v0 in a gravity free space as shown in figure. Collision between the rod and the ball is perfectly elastic. Then find the magnitude of velocity of ball after the collision ( neglect the friction between the ball and the rod during the collision ).
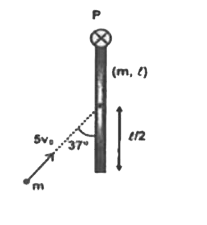 A√64949v0B√86549v0C√56349v0D√77249v0
A√64949v0B√86549v0C√56349v0D√77249v0 - Question 2 - Select One
In the figure, the block of mass m, attached to the spring of stiffness k is in correct with the completely elastic wall, and the compression in the spring is e. The spring is compressed further by e by displacing the block towards left and is then released. If the collision between the block and the wall is completely eleastic then the time period of oscillation of the block will be
 A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk
A2π3)√mkB(2π)√mkCπ3√mkDπ6√mk - Question 3 - Select One or More
In a perfectly elastic collision between two bodies
AKinetic energy of the system remains constant .BMechanical energy of the system remains constant .CKinetic energy first decreases and then ncreases .DKinetic energy before collision is equal to kinetic energy after collision .
The friction coefficient between the horizontal surface and each of the block shown in the figure is 0.2. The collision between the blocks is perfectly elastic. Find the separation between them when they come to rest. (Take g=10m/s2).
 View Solution
View SolutionFigure shown a block P of mass m resting on a smooth horizontal surface, attached to a spring of force constant k which is rigidly fixed on the wall on left side, shown in the figure . At a distance l to the right of the block there is a rigid wall. If block is pushed towards loft so that spring is compressed by a distance 5l/3 and when released, if will starts its oscillations. If collision of block with the wall is considered to be perfectly elastic. Find the time period of oscillation of the block.
 View Solution
View SolutionAn object is moving towards a mirror with a velocity of 10ms−1 as shown in the figure. If the collision between the mirror and the object is perfectly elastic, then the velocity of the image after collision with mirror in vector form is
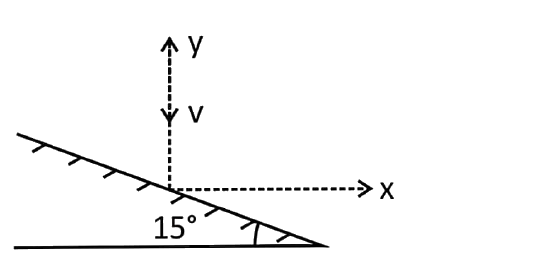 View Solution
View SolutionThree blocks of masses m , m and M are kept on a frictionless floor as shown in the figure .The leftmost block is given velocity v towards the right . All the collision between the blocks are perfectly inelastic . The loss in kinetic energy after all the collision is 5/6th of initial kinetic energy. The ratio of M/m will be
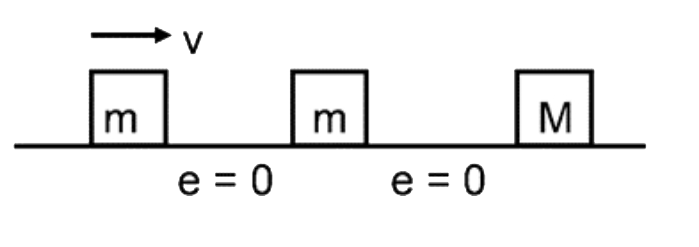 View Solution
View SolutionThe collision between both blocks shown in figure is completely inelastic. The total energy of oscillation after collision is
 View Solution
View Solution

