Solve the following initial value problem: drdt= −rt, r(0)=r0
Given differential equation {dr}{dt}=−rt
Find: Find the general solution of this differential equation.
={dr}{dt}=−r{t}
Integrating both side
=∫{d}r{r}=∫−{t}{dt}
=log|r|=−{t}22+C…………….({i})
Put t=0,r=r0 in equation (i).
Now, log|r0|=−0+C
log|r0|=C
Put the value of C in eq(i)
log|r|=−t22+log|r0|
=rr0=et22
Hence, r=r0et22
Topper's Solved these Questions
Similar Questions
Solve the following initial value problem: drdt= −rt, r(0)=r0
View SolutionSolve the following initial value problem: (1+y2)dx+(x−e−tan−1y)dy=0, y(0)=0
View SolutionVerify that each of the following functions y:R→R, as defined below, is the solution of the accompanying initial value problems :
y=cosx(x∈R):y''+y=0,y(0)=1,y'(0)=0.View SolutionVerify that each of the following functions y:R→R, as defined below, is the solution of the accompanying initial value problems :
y=ex:y'=y,y(0)=1View SolutionVerify that each of the following functions y:R→R, as defined below, is the solution of the accompanying initial value problems :
y=x2+2x+1,y'''=0,y(0)=1,y'(0)=2,y''(0)=2View SolutionLet (2x2+x+2x)n=r=t∑r=marxr, then answer the following.
(a) The value of m and t are …
(b) The value of r=t∑r=mar=…
(c ) The value of at=…
(d) The value of am=…
(e ) If ap=aq, then p+q=...
E=[1+2(x+1x)]n=r=t∑r=marxr,
where r=(m,m+1,...,t)
E=C0+C1.2(x+1x)+C2[2(x+1x)]2+......+Cn[2(x+1x)]n
=t∑r=marxrView SolutionSolve the foregoing problem for the case of two concentric spheres of radii R1 and R2 and temperatures T1 and T2.
View SolutionA soap bubble of radius 'r' and surface tension 'T' is given a potential of 'V' volt. If the new radiys 'R' of the bubble is related to its initial radius by equation.
P0[R3−r3]+[λT[R2−r2]−ε0V2R/2=0, where P0 is the atmospheric pressure. Then find λView Solution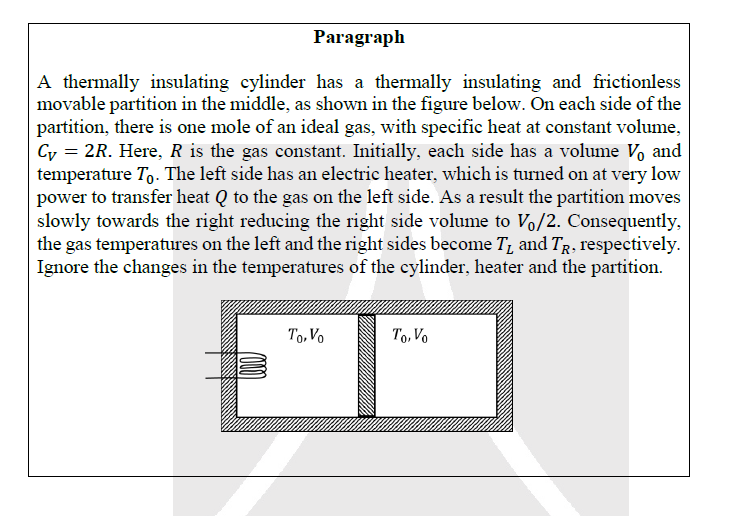 Value of QRT0View Solution
Value of QRT0View SolutionA soap bubble of radius r and surface tension T is given a potential V. Show that the new radius R of the bubble is related with the initial radius by the equation
P(R3−r3)+4T(R2−r2)=∈0V2R2 where P is the atmospheric pressure.View Solution

