What is the least possible integer value for which 40% of that integer is greater than 9.6?
4
The correct Answer is:D
Difficult:Medium:
Category: Heart of Algebra/ Inequalities
Strategic Advice: Sometimes, question are much easier than they sound. Translate from English into Math and you'll see that this question actually involves solving a fairly simple inequality.
Getting to the Answer: Call the unknown integer x. Translate "40% of that integer" as 0.4x. The rest is very straightforward: . Divide both sides of the inequality by 0.4 to find that .The question specifically says greater (not greater than or equal to ), so the correct answer is 25, which is (D).
Topper's Solved these Questions
Similar Questions
Knowledge Check
{:("Column A","q is an integer greater than 1. Let <q> stand for the smallest positive integer factor of q that is greater than 1.", "Column B"),(
,,):}
AIf column A is largerBIf column B is largerCIf the columns are equalDIf there is not enough information to decide
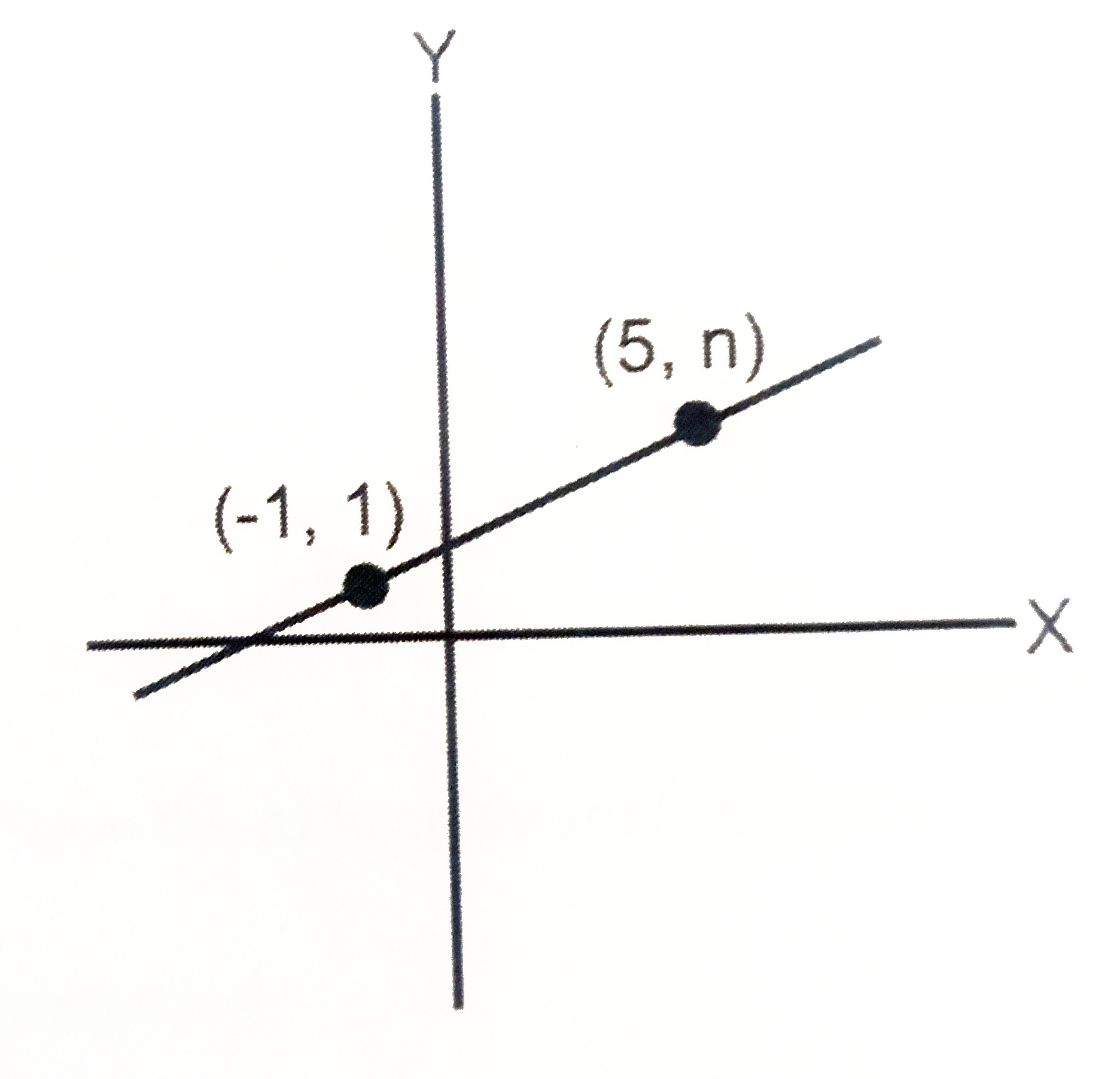
The graph above depicts a straight line passing through (-1, 1) and (5, n). What is the least integer value of n if the slope is greater than 23 ?
View SolutionWhat is the greatest integer value of x such that 1−2x is at least 6?
View SolutionWhich of the following statements are true? (i) The smallest integer is zero (ii) The opposite of zero is zero (iii) Zero is not an integer (iv) 0 is larger than every negative integer. (v) The absolute value of an integer is greater than the integer. (vi)A positive integer is greater than its opposite (vii)Every negative integer is less than every natural number. (viii)0 is the smallest positive integer.
View SolutionIf [x] is the greatest integer less than or equal to x and (x) be the least integer greater than or equal to x and [x]2+(x)2>25 then x belongs to
View SolutionThe sum of the areas of two squares is 85. If the sides of both squares have integer lengths, what is the least possible value for the length of a side of the smaller square?
View Solution(i) Write 4 negative integers less than −10 (ii) Write 6 negative integers just greater than −12
View SolutionFind the sum of the possible integer values of m:
2m+n=10
m(n−1)=9
View Solution
