The approximate height h of an object launched vertically upward after an elapsed time t is represented by the equation $h = \frac{1}{2} a t^{2} + v_{o} t + h_{o}$ , where a is acceleration due to gravity, $v_{o}$ is the object's initial velocity, and $h_{o}$ is the objects initial height. the table aabove gives the acceleration due to gravity on Earth's moon and several planets. If two identical objects launched vertically upward at an initial velocity of 40m/s from the surfaces of Mars and Earth's moon approximately how many more seconds will it take for the moon projectile to return to the ground than the Mars projectile?

A

$21$

B

$28$

C

$36$

D

$50$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Difficult: Medium
Category: Passport to Advanced Math/ Quadratics
Strategy Advice: For a question like this, you'll need to interpret what is being asked for. Here, "to reach the ground" means that the height, h, eqauls 0, so your goal is to find the times (solve for t) when h=0 for the two projectiles,and the find the difference between them
Getting to the Answer: You know both projectiles begin at their respective surfaces and will be launched vertically at 40m/s, so $h_{o} = 0 and v_{o} = 40$ for both . According to the table acceleration due to gravity on Mars is 3.7m/ $s^{2}$ , so the final for the height of the Mars projectile is $h_{Mars} = - 1.85 t^{2} + 40 t$ . Similarly, acceleration due to gravity on the moon is 1.6m/ $s^{2}$ , which makes the equation for the height of the moon projectile $h_{moon} = - 0.8 t^{2} + 40 t$ . Substitute 0 for h in each equation, and solve for t via factoring as follows:

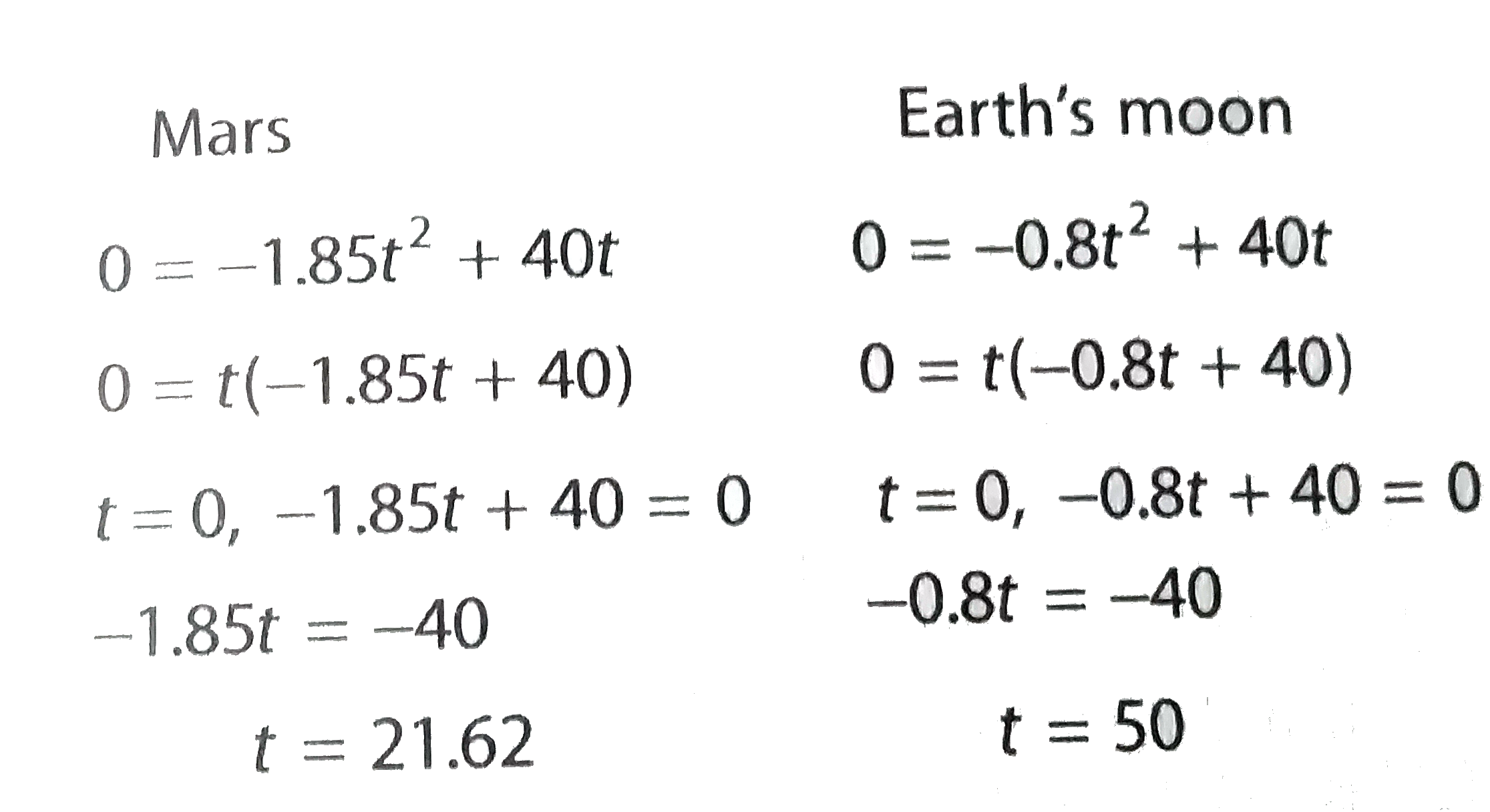
At t=0, the objects have not yet been launched, so disregard this value of t. Subtract the other values you found to get to the difference between the landing times, $50 - 21.62 = 28.38$ seconds. The closest answer choice is (B).
You could also graph the equations in a graphing calculator and use the trace or zero commands to determine when h=0.

|

Updated on:21/07/2023

Class 10 MATHS QUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An object lauched upwards at an angle has parabolic motion. The height h, of a projectile at time t is given by the equation $h = \frac{1}{2} a t^{2} + v_{y} t + h_{0},$ where a is the acceleration due to gravity, $v_{v}$ is the vertical component of the velocity, and $h_{0}$ is the initial height. Which of the following equations correctly represents the object's acceleration due to gravity in terms of the other variables ?
A $a = \frac{h - v_{v} t - h_{0}}{t}$
B $a = \frac{h - v_{v} t - h_{0}}{2 t^{2}}$
C $a = \frac{2 (h - v_{v} t - h_{0})}{t^{2}}$
D $a = t \sqrt{2 (h - v_{v} t - h_{0})}$
Question 2 - Select One
$h = - 4.9 t^{2} + 25 t$
The equation above expresses the approximate height h, in meters, of a ball t seconds after it is launched vertically upward from the ground with an initial velocity of 25 meters per second. After approximately how many seconds will the ball hit the ground?
A3.5
B $4.0$
C4.5
D $5.0$
Question 3 - Select One
The distance a free falling object has traveled can be modeled by the equation, $d = \frac{1}{2} a t^{2}$ where a is acceleration due to gravity and t is the amount of time the object has fallen. What is t in terms of a and d?
A $t = \sqrt{\frac{d a}{2}}$
B $t = \sqrt{\frac{2 d}{a}}$
C $t = {(\frac{d a}{2})}^{2}$
D $t = {(\frac{3 d}{a})}^{2}$

KAPLAN-QUADRATIC EQUATIONS AND THEIR GRAPHS-Multiple Choice Question

Home
Ask Doubt
Profile