Circle C (not shown) is drawn on a coordinate plane, centered at the origins. If the point (a, b) lies on the circumference of the circle, what is the radius of the cirle in terms of a and b?
a−b
a+b
√a2+b2
a2+b2
The correct Answer is:C
To find the radius of circle C centered at the origin (0, 0) in terms of the coordinates of a point (a, b) on its circumference, we can follow these steps:
1. Identify the Center of the Circle:
The center of the circle is given as the origin, which has coordinates (0, 0).
2. Identify the Point on the Circumference:
The point on the circumference of the circle is given as (a, b).
3. Use the Distance Formula:
The radius of the circle is the distance between the center and the point on the circumference. The distance d between two points (x1,y1) and (x2,y2) in a coordinate plane is calculated using the formula:
d=√(x2−x1)2+(y2−y1)2
4. Substitute the Coordinates into the Distance Formula:
Here, (x1,y1)=(0,0) (the center) and (x2,y2)=(a,b) (the point on the circumference). Plugging these values into the distance formula gives:
d=√(a−0)2+(b−0)2
5. Simplify the Expression:
This simplifies to:
d=√a2+b2
6. Conclusion:
Therefore, the radius r of the circle in terms of a and b is:
r=√a2+b2
Final Answer:
The radius of the circle in terms of a and b is r=√a2+b2.
---
The center of the circle is given as the origin, which has coordinates (0, 0).
The point on the circumference of the circle is given as (a, b).
The radius of the circle is the distance between the center and the point on the circumference. The distance d between two points (x1,y1) and (x2,y2) in a coordinate plane is calculated using the formula:
d=√(x2−x1)2+(y2−y1)2
Here, (x1,y1)=(0,0) (the center) and (x2,y2)=(a,b) (the point on the circumference). Plugging these values into the distance formula gives:
d=√(a−0)2+(b−0)2
This simplifies to:
d=√a2+b2
Therefore, the radius r of the circle in terms of a and b is:
r=√a2+b2
The radius of the circle in terms of a and b is r=√a2+b2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
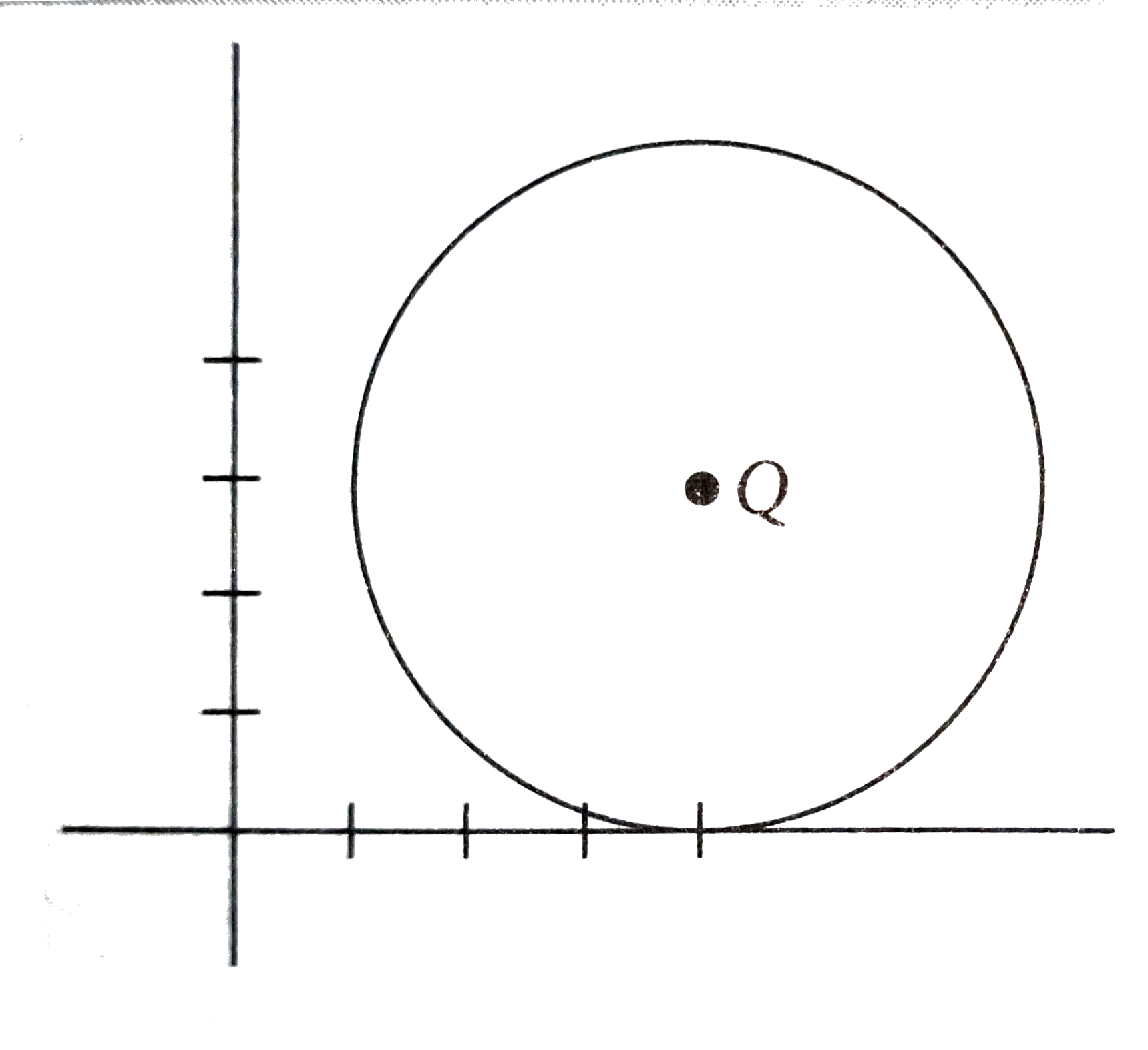
Center Q of the circle above has coordinate of (4,3). What is the circumference of the circle?AπB2πC6πD9π - Question 2 - Select One
The center of circle O (not shown) falls on the point where the line y=43x+4 intersects the x-axis on the coordinate plane. The point (3, 8) lies on the circumference of the circle. Which of the following could be the equation for circle O?
Ax2+y2=25B(x+3)2+y2=25C(x+3)2+y2=100D(x+3)2+(y−8)2=100 - Question 3 - Select One
In the figure, O is the center of the circle. What is average of the numbers a, b, c and d?
 A45B60C90D180
A45B60C90D180

Point O is the center of the circle above. What fraction of the circumference of the circle is the length of the bolded arc?View SolutionThe line 2x−y+1=0 is tangent to the circle at the point (2, 5) and the center of the circle lies on x−2y=4 . Then find the radius of the circle.
View SolutionWhat is the radius of a circle whose circumference is π?
View SolutionIn the xy-plane , a circle with center (6,0) is tangent to the line y=x. what is the radius of the circle ?
View Solution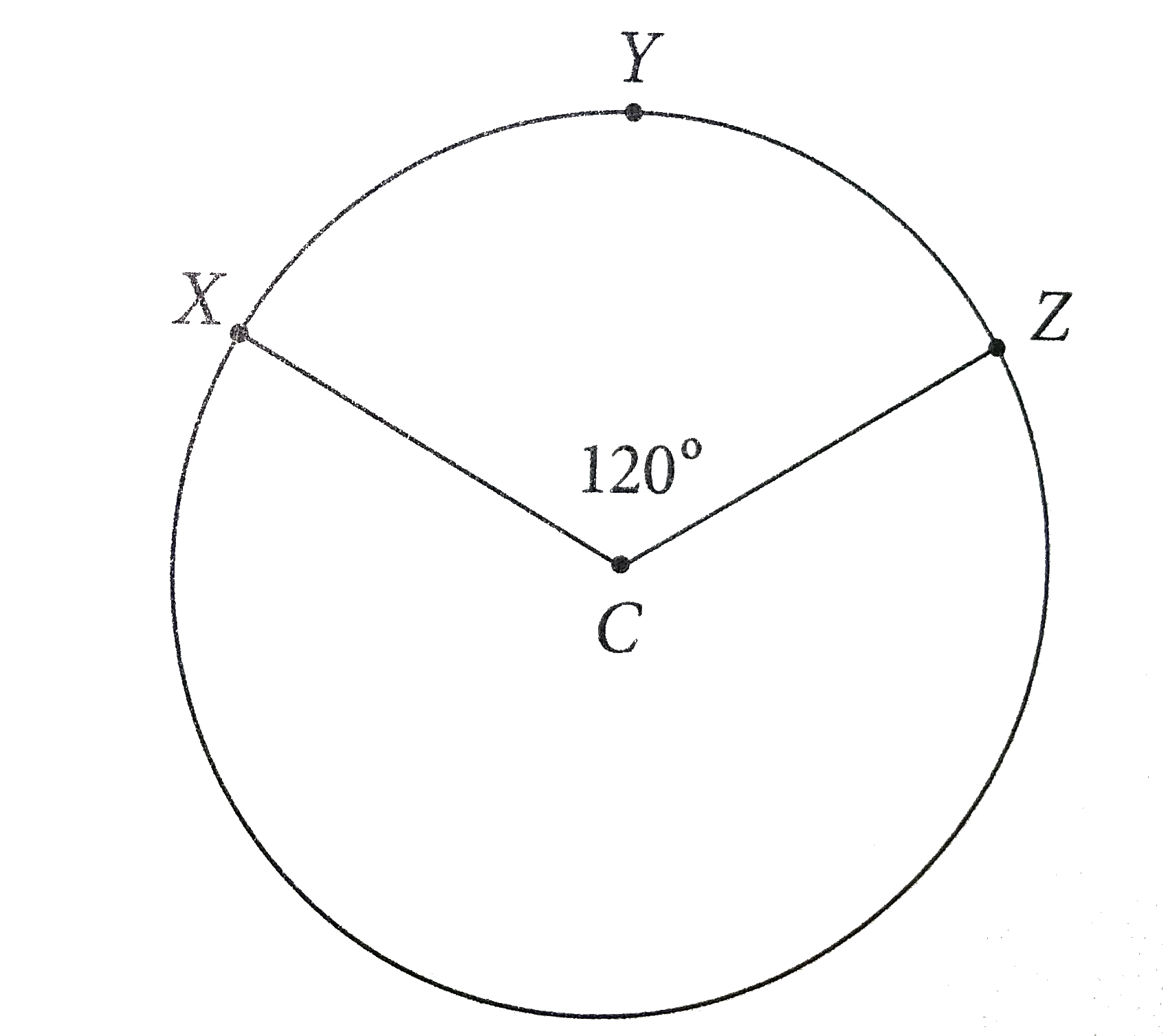
In the figure above, C is the center of a circle. If the length of the arc XYZ is 4π, what is the radius of the circle?View Solution


