Three rods of the same dimension have thermal conductivities 3K, 2K and K. They are arranged as shown in fig. with their ends at 100∘C,50∘C and 20∘C. The temperature of their junction is
60∘C
70∘C
50∘C
35∘C
To solve the problem of finding the temperature of the junction of three rods with different thermal conductivities and temperature ends, we can follow these steps:
1. Identify the Given Data:
- Thermal conductivities:
- Rod 1: 3K
- Rod 2: 2K
- Rod 3: K
- Temperatures at the ends:
- Rod 1: 100∘C
- Rod 2: 50∘C
- Rod 3: 20∘C
2. Assume the Temperature at the Junction:
- Let the temperature at the junction be T.
3. Write the Heat Current Equations:
- The heat current through each rod can be expressed using Fourier's law of heat conduction:
H=ΔTR
- Where R=LkA (length L, thermal conductivity k, and cross-sectional area A). Since the rods have the same dimensions, we can simplify our calculations by focusing on the temperature differences and thermal conductivities.
4. Set Up the Heat Current Balance:
- For rod 1 (conductivity 3K):
H1=T−100L3K=3K(T−100)L
- For rod 2 (conductivity 2K):
H2=T−50L2K=2K(T−50)L
- For rod 3 (conductivity K):
H3=T−20LK=K(T−20)L
5. Set the Total Heat Current to Zero:
- Since there is no heat generation, the sum of the heat currents must equal zero:
H1+H2+H3=0
- Substitute the expressions for H1, H2, and H3:
3K(T−100)L+2K(T−50)L+K(T−20)L=0
6. Simplify the Equation:
- Multiply through by L (which cancels out) and factor out K:
3(T−100)+2(T−50)+(T−20)=0
- Expand the equation:
3T−300+2T−100+T−20=0
- Combine like terms:
6T−420=0
7. Solve for T:
- Rearranging gives:
6T=420
- Dividing by 6:
T=70∘C
Final Answer:
The temperature of the junction is 70∘C.
- Thermal conductivities:
- Rod 1: 3K
- Rod 2: 2K
- Rod 3: K
- Temperatures at the ends:
- Rod 1: 100∘C
- Rod 2: 50∘C
- Rod 3: 20∘C
- Let the temperature at the junction be T.
- The heat current through each rod can be expressed using Fourier's law of heat conduction:
H=ΔTR
- Where R=LkA (length L, thermal conductivity k, and cross-sectional area A). Since the rods have the same dimensions, we can simplify our calculations by focusing on the temperature differences and thermal conductivities.
- For rod 1 (conductivity 3K):
H1=T−100L3K=3K(T−100)L
- For rod 2 (conductivity 2K):
H2=T−50L2K=2K(T−50)L
- For rod 3 (conductivity K):
H3=T−20LK=K(T−20)L
- Since there is no heat generation, the sum of the heat currents must equal zero:
H1+H2+H3=0
- Substitute the expressions for H1, H2, and H3:
3K(T−100)L+2K(T−50)L+K(T−20)L=0
- Multiply through by L (which cancels out) and factor out K:
3(T−100)+2(T−50)+(T−20)=0
- Expand the equation:
3T−300+2T−100+T−20=0
- Combine like terms:
6T−420=0
- Rearranging gives:
6T=420
- Dividing by 6:
T=70∘C
The temperature of the junction is 70∘C.
Topper's Solved these Questions
Similar Questions
Three rods of the same dimension have thermal conductivities 3K, 2K and K. They are arranged as shown in fig. Given below, with their ends at 100∘C,50∘C and 20∘C. The temperature of their junction is :-

View SolutionThree rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below

Then , the temperature of the junction in steady - state is
View Solution
Knowledge Check
Three rods of the same dimensions have thermal conductivities 3k , 2k and k . They are arranged as shown, with their ends at 100∘C,50∘C and 0∘C. The temperature of their junction is :-
_E01_022_Q01.png) A75∘CB2003∘CC40∘CD1003∘C
A75∘CB2003∘CC40∘CD1003∘CThree rods of same dimensions have thermal condutivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
 .A2003∘CB1003∘CC75∘CD81∘C
.A2003∘CB1003∘CC75∘CD81∘CThree rods of same dimensions have thermal condutivity 3K,2K and K They are arranged as shown in Then the temperature of the junction in steady state is
 .A2003.∘CB1003.∘CC75∘CD503.∘C
.A2003.∘CB1003.∘CC75∘CD503.∘C
Three rods of same dimensions have thermal conductivities 3K, 2k and K, with their ends at 100∘C,50∘Cand0∘C respectively . They re arranged as shown in the diagram . The temperature of the junction J in steady -state is
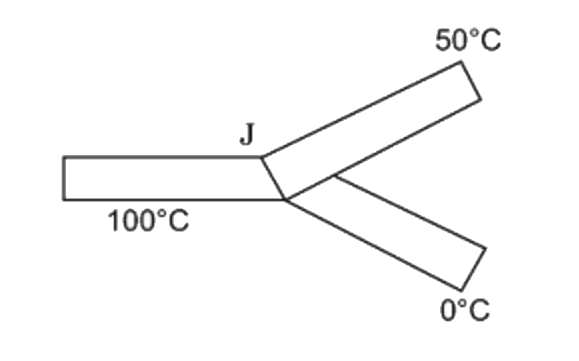
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is
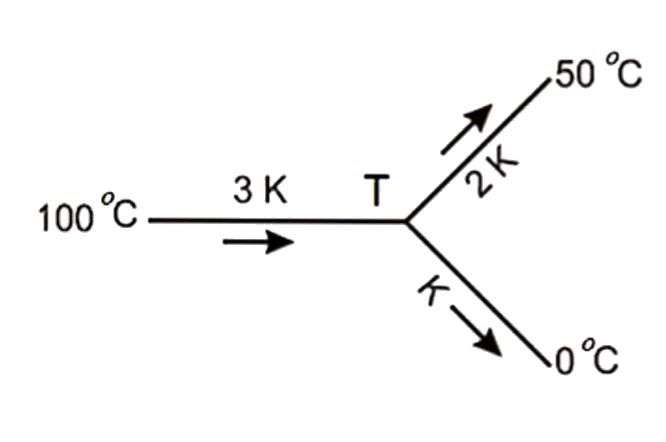
View SolutionTwo rods of same dimensions, but made of different materials are joined end to end to end with their free end being maintained at 100∘C and 0∘C respectively. The temperature of the junction is 70∘C. Then the temperature of the junction if the rods are inerchanged will be equal to T∘C Find T:
View SolutionThree rods of the same dimension have thermal conductivity 3K, 2K and K as shown in the figure. The temperature of the junction in steady-state is

View SolutionA metallic prong consists of 4 rods made of the same material, cross-section and same lengths as shown. The three forked ends are kept at 100∘C and the handle end is at 0∘C. The temperature of the junction is
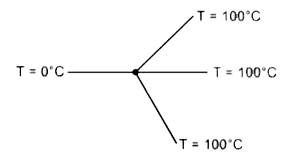
View Solution
