The (x,y) co-ordinates of the corners of a square plate are (0,0), (L,L) and (0,L). The edges of the plate are clamped and transverse standing waves are set up in it. If u(x,y) denotes the displacement of the plate at the point (x,y) at some instant of time, the possible expression (s) for u is (are) (a=positiveconstant)
1,2 and 3 are correct
1 and 2 are correct
2 and 4 are correct
1 and 3 are correct
Step by step video & image solution for The (x, y) co-ordinates of the corners of a square plate are (0, 0), (L, L) and (0, L). The edges of the plate are clamped and transverse standing waves are set up in it. If u(x, y) denotes the displacement of the plate at the point (x, y) at some instant of time, the possible expression (s) for u is (are) (a = positive constant) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
If the image of the point (1,2,3) in the plane x+2y=0 is (h,k,l)then l=
View SolutionA wave pulse is travelling on a string at 2 m/s. displacement y of the particle at x = 0 at any time t is given by
y=2t2+1
Find
(i) Expression of the function y = (x, t) i.e., displacement of a particle position x and time t.View Solution
Knowledge Check
- Question 1 - Select One
If co-ordinates of a moving point at time t are given by x=a (l+sint) and y=a(1−cost), then:
Athe slope of accelration time graph is zeroBthe slope of velocity-time graph is constnatCthe direction of motion makes an angle t/2 with x-axisDall of the above - Question 2 - Select One or More
For a certain transverse standing wave on a long string , an antinode is formed at x=0 and next to it , a node is formed at x=0.10m , the displacement y(t)of the string particle at x=0 is shown in Fig.7.97.
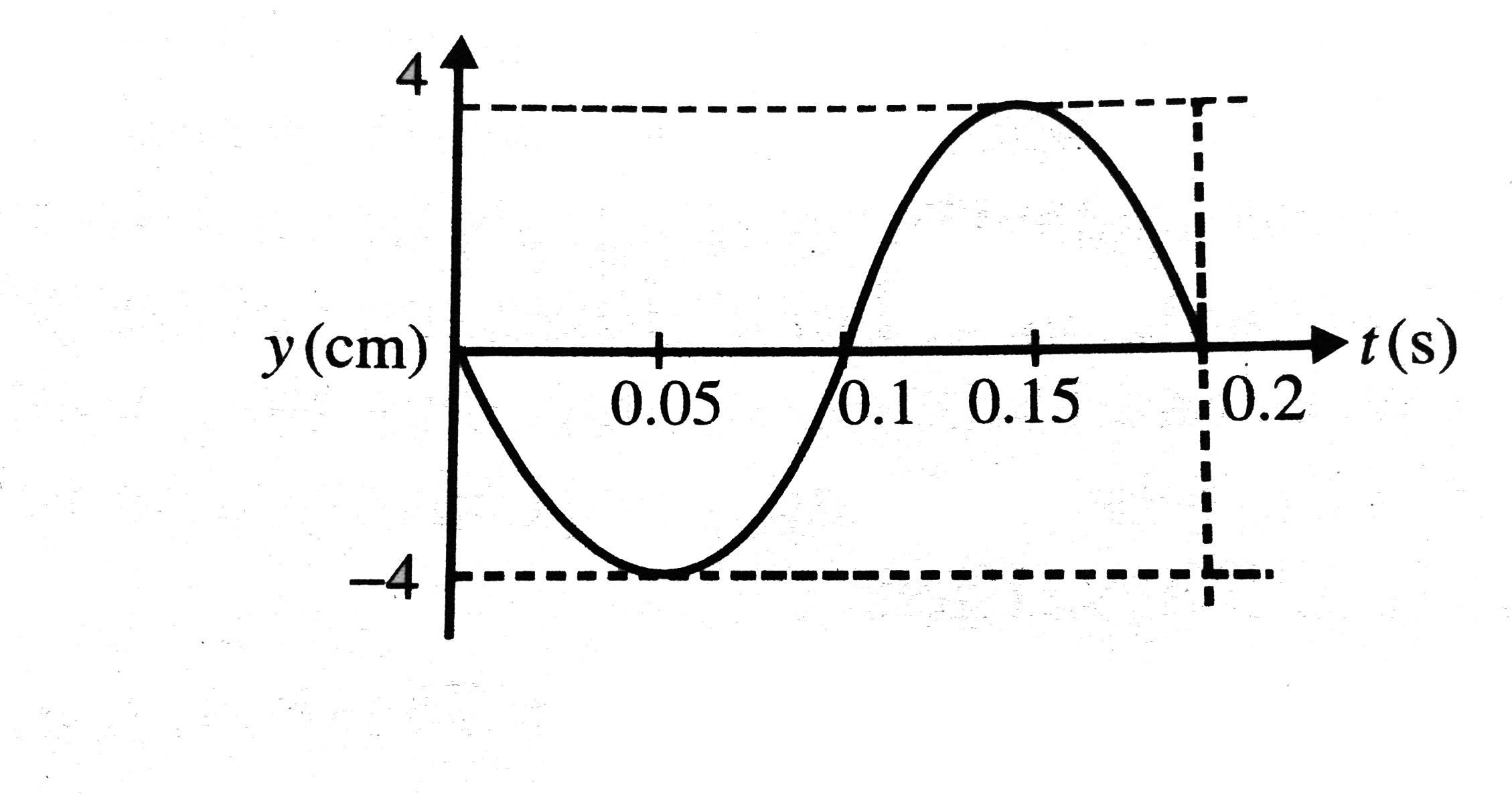ATransverse displacement of the particle at x=0.05m and t=0.05sis−2√2cmBTransverse displacement of the particle at x=0.04m and t=0.025sis−2√2cmCSpeed of the travelling waves that interface to produce this standing wave is 2m/sDThe transverse velocity of the string particle at x=1/15m and t=0.1sis20πcm/s - Question 3 - Select One
The standing wave in a medium is expressed as y=0.2sin(0.8x)cos(3000t)m. The distance between any two consecutive points of minimum of maximum displacement is
Aπ2mBπ4mCπ6mDNone of these
The length of the chord intercepted on the line 2x-y+2=0 by the parabola x2=8y is l then l=
View SolutionThe standing waves are set up by the superimposition of two waves:
y1=0.05sin(15πt−x)and
y2=0.05sin(15πt+x), where x and y are in metre and t in seconds. Find the displacement of particle at x=0.5m.View SolutionA uniform rectangular plate has side length l and 2l. The plate is in x−y plane with its centre at origin and sides parallel to x and y axes. The moment of inertia of the plate about an axis passing through a vertex (say A) perpendicular to the plane of the figure is I0. Now the axis is shifted parallel to itself so that moment of inertia about it still remains I0. Write the locus of point of intersection of the axis with xy plane
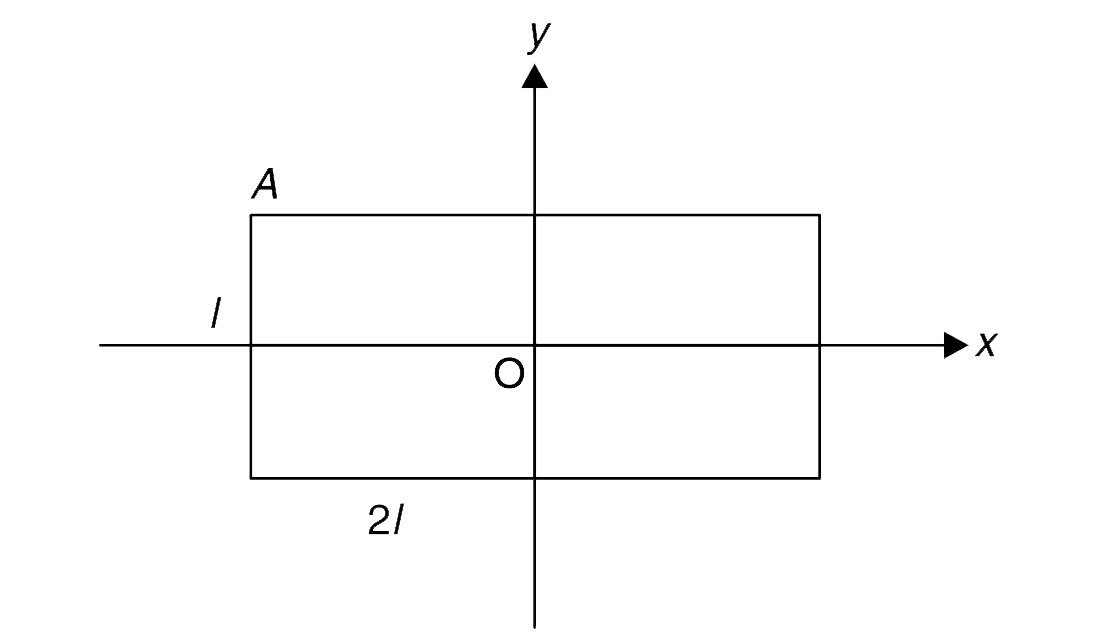View SolutionA parallel plate capacitor has square plates of side length L. Plates are kept vertical at separation d between them. The space between the plates is filled with a dielectric whose dielectric constant (K) changes with height (x) from the lower edge of the plates as K=eβx where b is a positive constant. A potential difference of V is applied across the capacitor plates.
(i) Plot the variation of surface charge density (s) on the positive plate of the capacitor versus x.
(ii) Plot the variation of electric field between the plates as a function of x.
(iii) Calculate the capacitance of the capacitor.
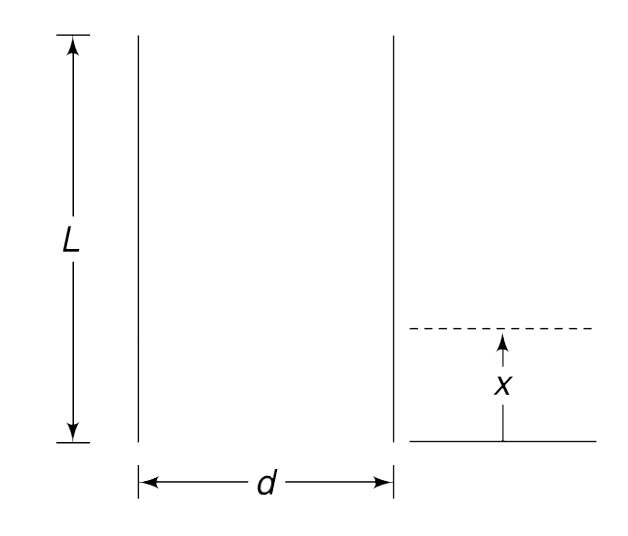View Solutionx and y co-ordinates of a particle moving in x−y plane at some instant of time are x=2t and y=4t.Here x and y are in metre and t in second. Then
The path of the particle is a…….View Solution