elocity at a general point P(x, y) for a horizontal projectile motion is given by
v=√(v2x+vy2),tanα=vyvx 
αis angle made by v with horizontal in clockwise direction Trajectory equation for a horizontal projectile motion is given by x=vxt=ut
y=-(1/2)gt2 
eliminating t, we get y=−(1/2)gx2u2
5An aeroplane is in a level flying at an speed of 144 km//hr at an altitude of 1000 m. How far horizontally from a given target should a bomb be released from it to hit the target ?
571.43
671.43
471.34
371.34
Step by step video & image solution for elocity at a general point P(x, y) for a horizontal projectile motion is given by v=sqrt((v_("x")^(2)+v_("y")"^(2))),tan alpha=(v_(y))/(v_(x)) alphais angle made by v with horizontal in clockwise direction Trajectory equation for a horizontal projectile motion is given by x=v_(x)t=ut y=-(1//2)"gt"^(2) eliminating t, we get y=-(1//2)(gx^(2))/(u^(2) 5An aeroplane is in a level flying at an speed of 144 km//hr at an altitude of 1000 m. How far horizontally from a given target should a bomb be released from it to hit the target ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Velocity at a general point P(x, y) for a horizontal projectile motion is given by
v=√(v2x+vy2),tanα=vyvx
αis angle made by v with horizontal in clockwise direction Trajectory equation for a horizontal projectile motion is given by x=vxt=ut
y=-(1/2)gt2
eliminating t, we get y=−(1/2)gx2u2
An aeroplane is flying horizontally with a velocity of 720 km/h at an altitude of 490 m. When it is just vertically above the target a bomb is dropped from it. How far horizontally it missed the target?
View SolutionVelocity at a general point P(x, y) for a horizontal projectile motion is given by
v=√(v2x+vy2),tanα=vyvx
αis angle made by v with horizontal in clockwise direction Trajectory equation for a horizontal projectile motion is given by x=vxt=ut
y=-(1/2)gt2
eliminating t, we get y=−(1/2)gx2u2
A ball rolls off top of a stair way with a horizontal velocity u m//s. If the steps are h m high and b meters wide, the ball will just hit the edge of nth step if n^(th) equals to
View Solution
Knowledge Check
The equations of motion of a projectile are given by x=36tm and 2y=96t−9.8t2m .The angle of projection is
Asin−1(45)Bsin−1(35)Csin−1(43)Dsin−1(34)The electric potential at a point (x,y,z) is given by V=−s2
A→E=ˆi(2xy−z3)+ˆjxy2+ˆk3z2xB→E=ˆi(2xy+z3)+ˆjx2+ˆk3xz2C→E=ˆi2xy+ˆj(x2+y2)+ˆk(3xz−y2)D→E=ˆiz+ˆjxyz+ˆkz2The electrostatic potential V at any point (x, y, z) in space is given by V=4x2
AThe y- and z-components of the electrostatic field at any point are zeroBThe x-component at any point is given by (−8xˆi)CThe x-component at (1, 0, 2) is (-8i)DThe y- and z-components of the field are constants in magnitude
The equations of motion of a projectile are given by x=36tm and 2y=96t−9.8t2m .The angle of projection is
View SolutionTrajectory of particle in a projectile motion is given as: y=x−(x2/80) (x and y are in meters). Take g=10m/s2.

View SolutionTrajectory of a particle in a projectile motion is given as y=x−x280. Here x and y are in metre. For this projectile motion the following with g=10m/s2.
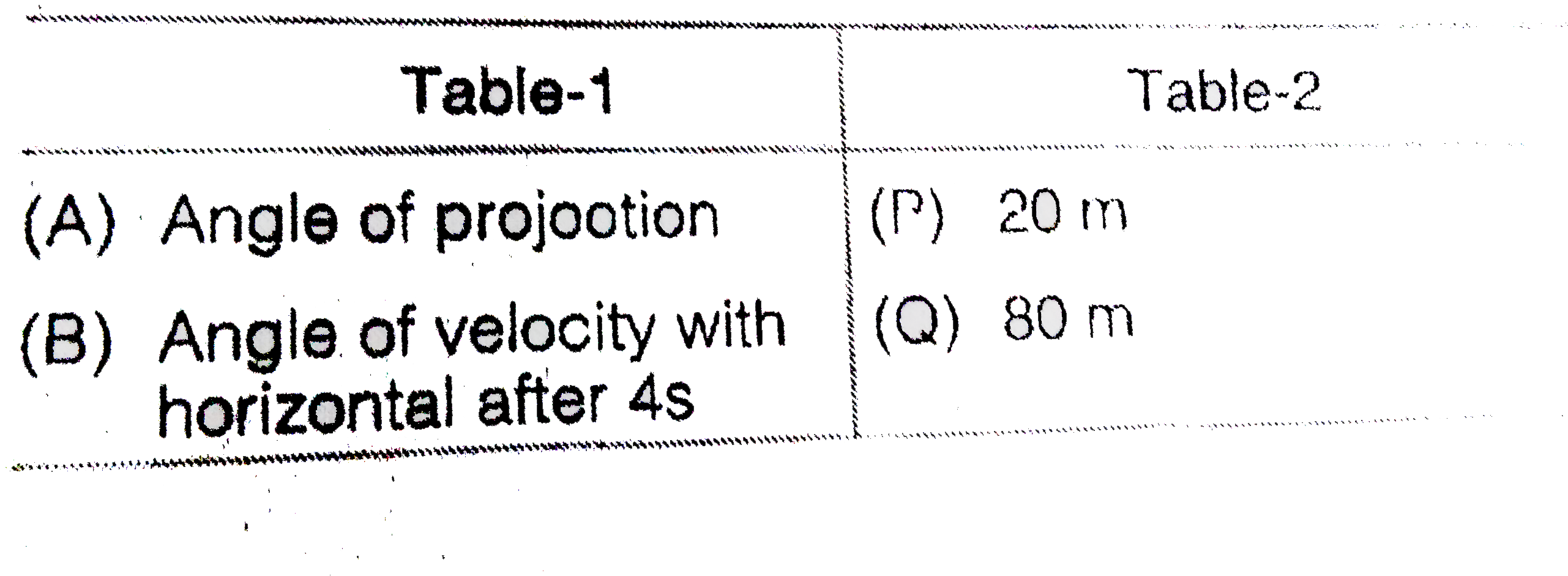
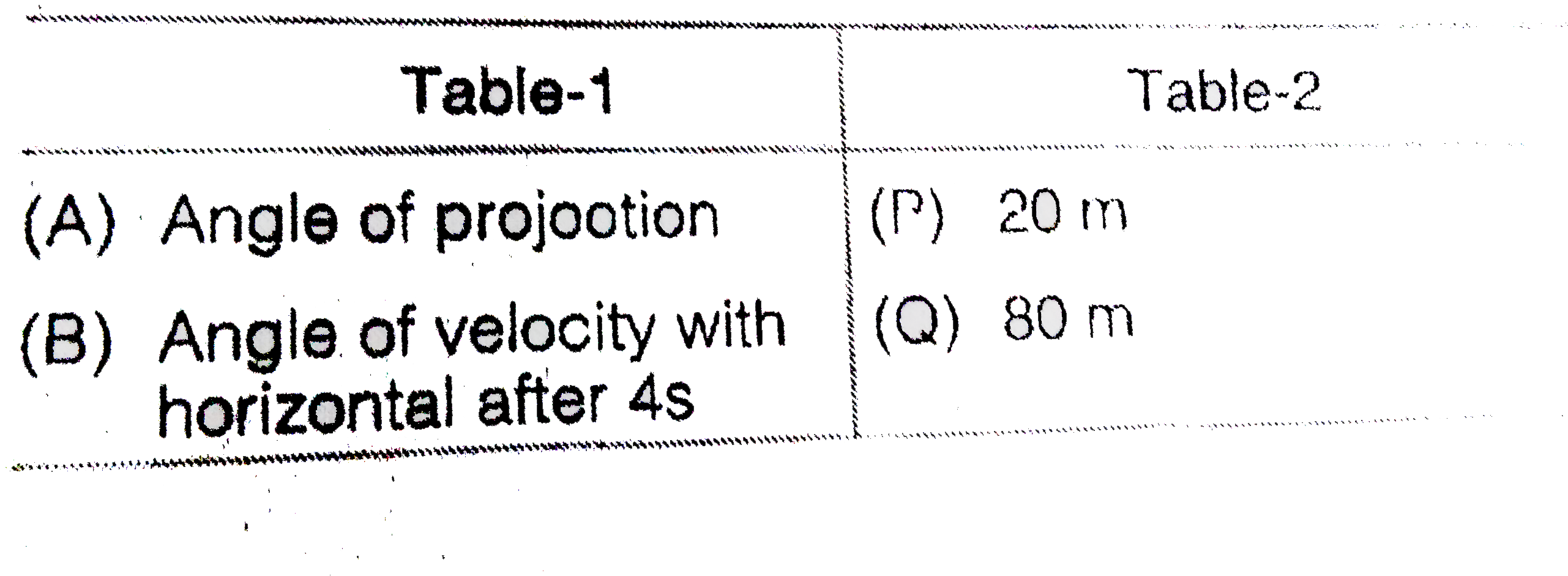
View SolutionIn a projectile motion, the height y=√3t−5t2+r3 and horizontal distance x=t+2t2−t3 . The angle of projection is given by
View SolutionThe horizontal and vertical displacements x and y of a projectile at a given time t are given by x=6tandy=8t−5t2 meter.The range of the projectile in metre is:
View Solution