A battery charges a parallel plate capacitor of thickness (d) so that an energy [U0] is stored in the system. A slab of dielectric constant (K) and thickness (d) is then introduced between the plates of the capacitor. The new energy of the system is given by
KU0
K2U0
U0K
U0/K2
The correct Answer is:A
To solve the problem, we need to analyze the situation step by step.
Step 1: Understand the Initial Energy Stored in the Capacitor
The initial energy stored in the capacitor, when it is charged by a battery, is given by the formula:
U0=12CV2
where C is the capacitance of the capacitor and V is the voltage across it.
Step 2: Determine the Capacitance of the Capacitor
For a parallel plate capacitor, the capacitance C is given by:
C=ϵ0Ad
where ϵ0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
Step 3: Introduce the Dielectric Material
When a dielectric slab with dielectric constant K and thickness d is introduced between the plates of the capacitor, the capacitance changes. The new capacitance C′ becomes:
C′=Kϵ0Ad
This is because the presence of the dielectric increases the capacitance by a factor of K.
Step 4: Calculate the New Energy Stored in the Capacitor
The new energy stored in the capacitor with the dielectric slab introduced is given by:
U′=12C′V2
Substituting C′ into the equation:
U′=12(Kϵ0Ad)V2
Step 5: Relate the New Energy to the Old Energy
Now, we can express the new energy U′ in terms of the old energy U0:
U′=K(12ϵ0AdV2)=KU0
Thus, the new energy stored in the capacitor after introducing the dielectric is:
U′=KU0
Final Answer
The new energy of the system after introducing the dielectric is:
U′=KU0
---
The initial energy stored in the capacitor, when it is charged by a battery, is given by the formula:
U0=12CV2
where C is the capacitance of the capacitor and V is the voltage across it.
For a parallel plate capacitor, the capacitance C is given by:
C=ϵ0Ad
where ϵ0 is the permittivity of free space, A is the area of the plates, and d is the separation between the plates.
When a dielectric slab with dielectric constant K and thickness d is introduced between the plates of the capacitor, the capacitance changes. The new capacitance C′ becomes:
C′=Kϵ0Ad
This is because the presence of the dielectric increases the capacitance by a factor of K.
The new energy stored in the capacitor with the dielectric slab introduced is given by:
U′=12C′V2
Substituting C′ into the equation:
U′=12(Kϵ0Ad)V2
Now, we can express the new energy U′ in terms of the old energy U0:
U′=K(12ϵ0AdV2)=KU0
Thus, the new energy stored in the capacitor after introducing the dielectric is:
U′=KU0
The new energy of the system after introducing the dielectric is:
U′=KU0
Topper's Solved these Questions
Similar Questions
A 2V battery is connected to a parallel plate capacitor of capacitance 4μF having its plated 5 cm apart. A dielectric of dielectric constant twice that of mica and thickness 3 cm is introduce between the plates of the capacitor. The additional charge that flows into the capacitor from the batter is .................μC.
View SolutionA parallel-plate capacitor of plate area A and plate separation d is charged by a ideal battery of e.m.f. V and then the battery is disconnected. A slab of dielectric constant 2k is then inserted between the plates of the capacitor so as to fill the whole space between the plates. Find the change in potential energy of the system in the process of inserting the slab.
View Solution
Knowledge Check
A parallel plate condenser with plate separation d is charged with the help of a battery so that U0 energy is stored in the system. A plate of dielectric constant K and thickness d is placed between the plates of condenser while battery remains connected. The new energy of the system will be-
AKU0BK2U0CU0KDU0K2Separation between the plates of a parallel plate capacitor is d and the area of each plates is A. When a slab of material of dielectric constant k and thickness t(t<d) is introduced between the plates. Its capacitance becomes
Aε0Ad+t(1−1k)Bε0Ad+t(1+1k)Cε0Ad−t(1−1k)Dε0Ad−t(1+1k)A parallel capacitor of capacitance C is charged and disconnected from the battery. The energy stored in it is E. If a dielectric slab of dielectric constant 6 is inserted between the plates of the capacitor then energy and capacitance will become.
A6E,6CBE,CCE/6,6CDE,6C
A parallel - plate capacitor of plate area Aand plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
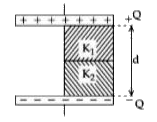
View SolutionA parallel-plate capacitor with plate area A has separation d between the plates. Two dielectric slabs of dielectric constant K1 and K2 of same area A/2 and thickness d/2 are inserted in the space between the plates. The capacitance of the capacitor will be given by :
View SolutionThe two plates of a parallel plate capacitor are 4mm apart. A slab of dielectric constant 3 and thickness 3mm is introduced between the plates is so adujected that the capacitance of the capacitor becomes 23rd of its original value. What is the new distance between the plates ?
View SolutionThe separation between the plates of a parallel plate capacitor is d and the area of each plate is A. iff a dielectric slab of thickness x and dielectric constant K is introduced between the plates, then the capacitance will be
View SolutionA parallel plate capacitor of plate area A and plate separation d is charged to potential difference V and then the battery is disconnected. A slab of dielectric constant K is then inserted between the plates of the capacitor so as to fill the space between the plates. If Q, E and W denote respectively, the magnitude of charge on each plate, the electric field between the plates (after the slab is inserted), and work done on the system, in question, in the process of inserting the slab, then
View Solution