A point object is placed on the principal axis of a concave mirror quite far away from the pole and moved at a constant speed 0.5cm/sec towards the pole. Its image also moves. It is found that the object and the image cross each other at a point which is at a distance 50 cm from the pole. Focal length of the mirror is -
50 cm
35 cm
25 cm
15 cm
The correct Answer is:C
To find the focal length of the concave mirror given the conditions of the problem, we can follow these steps:
Step 1: Understand the setup
We have a point object placed far away from the concave mirror and moving towards it at a constant speed of 0.5 cm/sec. The image of the object also moves, and they cross each other at a point 50 cm from the pole of the mirror.
Step 2: Use the mirror formula
The mirror formula relates the object distance (u), image distance (v), and focal length (f) of a mirror:
1f=1u+1v
Step 3: Identify distances
When the object and image cross at a distance of 50 cm from the pole, we can denote this distance as:
- v=−50 cm (the image distance is negative for concave mirrors)
- The object distance u will be equal to −2f when they meet at this point.
Step 4: Set up the equation
Since the object and image cross each other at 50 cm from the pole, we can set:
u=−50 cm (when they cross)
Using the mirror formula:
1f=1u+1v
Substituting u=−50 cm and v=−50 cm:
1f=1−50+1−50
1f=−150−150=−250=−125
Step 5: Solve for focal length
Taking the reciprocal gives us:
f=−25 cm
Conclusion
The focal length of the concave mirror is −25 cm.
---
We have a point object placed far away from the concave mirror and moving towards it at a constant speed of 0.5 cm/sec. The image of the object also moves, and they cross each other at a point 50 cm from the pole of the mirror.
The mirror formula relates the object distance (u), image distance (v), and focal length (f) of a mirror:
1f=1u+1v
When the object and image cross at a distance of 50 cm from the pole, we can denote this distance as:
- v=−50 cm (the image distance is negative for concave mirrors)
- The object distance u will be equal to −2f when they meet at this point.
Since the object and image cross each other at 50 cm from the pole, we can set:
u=−50 cm (when they cross)
Using the mirror formula:
1f=1u+1v
Substituting u=−50 cm and v=−50 cm:
1f=1−50+1−50
1f=−150−150=−250=−125
Taking the reciprocal gives us:
f=−25 cm
The focal length of the concave mirror is −25 cm.
Topper's Solved these Questions
Similar Questions
An object is placed o the principal axis of concave mirror of focal length 10 cm at a distance of 8.0 cm from the pole. Find the position and the nature of the image.
View SolutionA 2.0 cm high object is placed on the principal axis of a concave mirror at a distance of 12 cm from the pole. If the image is inverted, real and 5.0 cm high, find the location of the image the focal length of the mirror.
View Solution
Knowledge Check
- Question 1 - Select One
An object is present on the principal axis of a concave mirror at a distance 30cm from it. Focal length of mirror is 20cm.
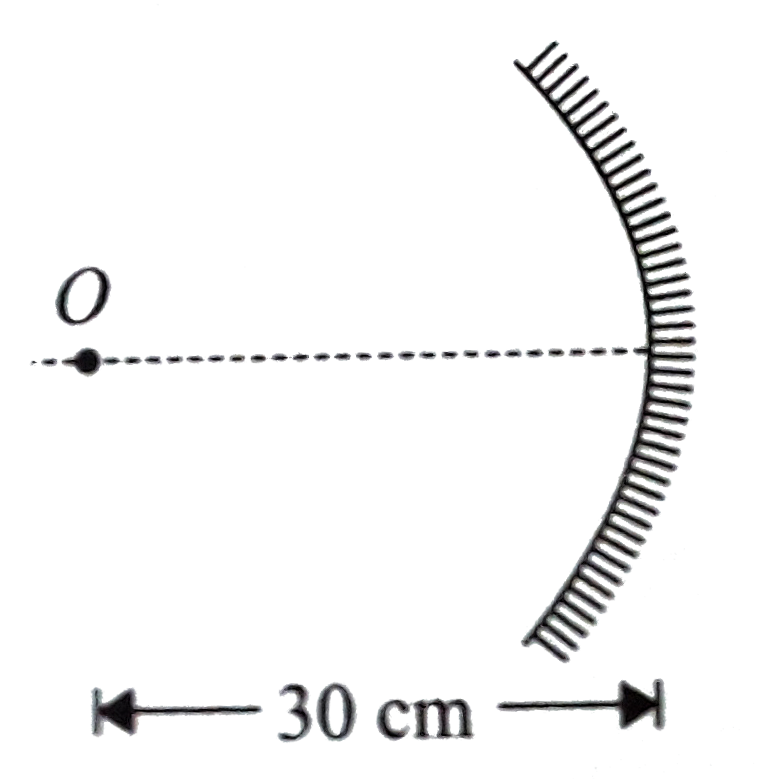
Q. Image formed by mirror isAAt a distance of 60cm in front of mirrorBAt a distance 60cm behind the mirrorCAt a distance 12 cm in front of mirrorDAt a distance 12cm behind the mirror - Question 2 - Select One
An object is present on the principal axis of a concave mirror at a distance 30cmfrom it.Focal length of mirror is20cm
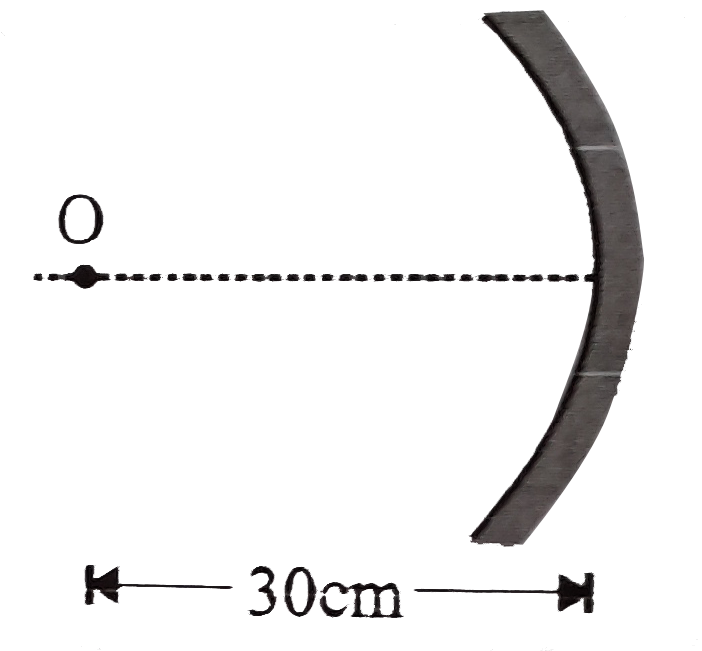
Image formed by mirror isAAt a distance 60cmin front of mirror.BAt a distance 60cmbehind of mirror.CAt a distance 12cmin front of mirror.DAt a distance 12cmbehind of mirror. - Question 3 - Select One
An object is placed at the center of curvature of a concave mirror. The distance between image and pole is:
AEqual to fBEqual to 2fCgreater than f but less than 2fDgreater than 2f
A point object is placed on the principal axis of a concave mirror of focal length 20 cm. At this instant object is given a velocity v towards the axis (event-I) or perpendicular to axis (event-2). Then, speed of image
 View Solution
View SolutionA point object is moving on the principal axis of a concave mirror of focal length 24cm towards the mirror. When it is at a distance of 60cm from the mirror, its velocity is . 9sec/cm What is the velocity of the image at that instant
View SolutionThe image of an object placed on the principal axis of a concave mirror of focal length 12 cm is formed at a point which is 10cm more distance form the mirror than the object. The magnification of the image is
View SolutionAn object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View SolutionAn object is placed at 20 cm from a convex mirror of focal length 20 cm. The distance of the image from the pole of the mirror is
View Solution

