A heavy particle is tied to the end A of a string of length 1.6 m. its other end O is fixed. It revolves as a conical pendulum with the string making 60C with the vertical then (g=10ms2)
its period of revolution is 2√2π5 sec.
The tension in the string is double the weight of the particle.
the velocity of the particle =√24ms
the centripetal acceleration of the particle is 10√3ms2.
The correct Answer is:A, B, C, D
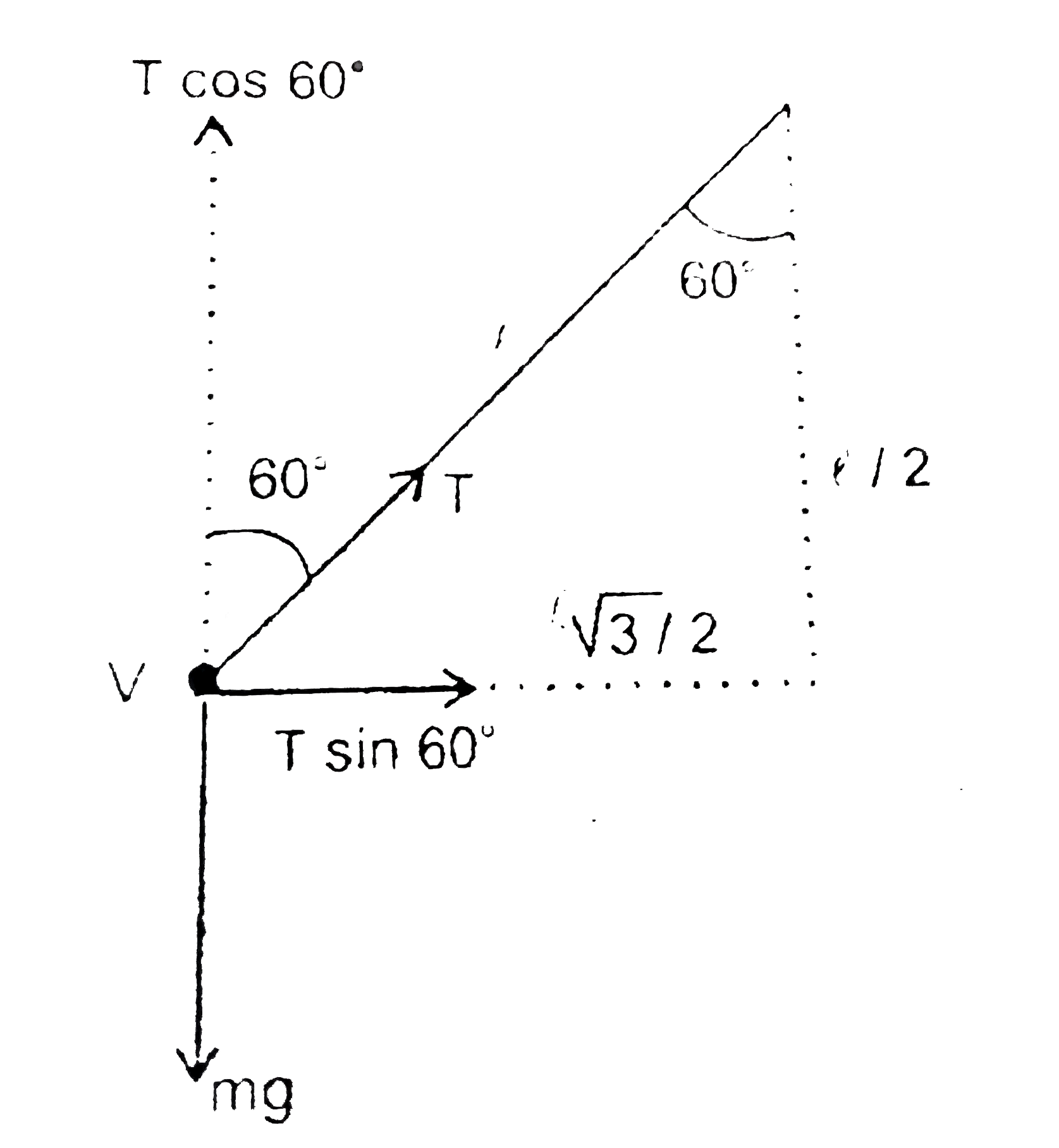
T√32=mv2(l√32) …(1)
T2=mg … (2)
Hence T=2mg, so (B) holds
From (1) & (2) V2=3gl2
∵C=√3×10×1.62
∵V=√24ms2 So (C) hold
aC=V2lr=(3gl2)(l√32)=10√3
∵ (D) holds
t=2πrv
t=2√2π5∵ (A) holds
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-0130videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-0230videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS107videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS127videos
TEST SERIES
Similar Questions
A heavy particle is tied ot the end A of a string of length 1.6m. Its other end O is fixed. It revolves as a conical pendulum with the string making 60∘ with the vertical. Then (g=10m/s2)
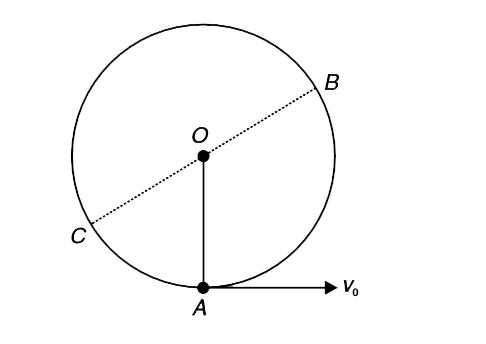
View SolutionA heavy particle is attached to one end of a light string of length l whose other end is fixed at O. The oarticle is projectyed horizontally with a velocity v0 from its lowest position A. When the angular displacement of the string is more than90∘, the particle leaves the circular path at B. The string again becomes taut at C such that B,O,C are collinear. Find v0 in terms of l and g
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A heavy particle is tied to the end A of a string of the length1.6 m. Its other end O is fixed. It revolves as a conical pendulum with the string making 60∘ with the horizontal. Then,
Aits period of revolution is 4π7sBthe tension is the string is 1√3 times the weight of the particleCthe speed of the particle is 2.8√3ms−1Dthe centripetal acceleration of the particle is 9.8√3ms−2 - Question 2 - Select One or More
A heavy particle is attached to one end of a string 1m long whose other end is fixed at O. It is projected from it lowest position horizontally with a velocity V:
AIf V2>5 g the particle will describe complete circular motion in the vertical planeBIf V2=3.5 g the tension in the string will become zero after the string has turned through 120∘CIf V2=2 g, the tension in the string becomes zero the velocity of the particle also becomes zeroDIf V2=g the velocity of the particle becomes zero after the string turns through 60∘ - Question 3 - Select One
A heavy small sized sphere is suspended by a string of length 2. The sphere is rotated uniformly in a horizontal circle with the string making an angle θwith the vertical. The time period of this conical pendulum is
A2π√ltanθgB2π√lcosθgC2π√1gD2π√lcosθg
A small brass bob is revolving in a horizontal circle with a constant speed of 2ms−1 at the end of a string of length 1 m. Find the time required for one revolution of the body. What angle does the string make with the vertical ?
View SolutionA body of mass m hangs at one end of a string of length l , the other end of which is fixed. It is given a horizontal velocity so that the string would just reach where it makes an angle of 60∘ with the vertical. The tension in the string at mean position is
View SolutionA body of mass m hangs at one end of a string of lenth l, the other end of which is fixed. It is given a horizontal velocity so that the string would just reach where it makes an angle of 60∘ with the vertical. The tension in the string at bottommost point position is
View SolutionA stone of mass 1 kg tied at the end of a string of length 1 m and is whirled in a verticle circle at a constant speed of 3ms−1. The tension in the string will be 19 N when the stone is (g=10ms−1)
View SolutionA heavy small sized sphere is suspended by a string of length l . The sphere rotates uniformly in a horizontal circle with the string making an angle θ with the vertical. Then the time period of this conical pendulum is-
View Solution

