A person throws a ball in vertical plane such that velocity of ball along horizontal is Vx and along vertical is vγ. Coefficinet of friction between man and gound is μ. Necessary condition so that man always remains at rest will be (Note: the process is done in time Δo0)
vx>μvγ
vx≤μvγ
vy≤μvx
μvx≤vy
The correct Answer is:B

JN=mvy
Jf≤μJN
mvx≤μmvy⇒vyvx≥1μ
μvy≥vx
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PT-0130videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - Pt-0230videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS107videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - PHYSICS127videos
TEST SERIES
Similar Questions
A ball rolls without sliding over a rough horizontal floor with velocity v0=7m/s towards a smooth vertical wall. If coefficient of restitution between the wall and the ball is e=0.7. Calculate velocity v of the ball long after the collision.
View SolutionA block of mass m is projected up with a velocity v0 along an inclined plane of angle of inclination θ=37∘. The coefficient of friction between the inclined plane AB and blocks is μ(=tanθ). Find the values of v0 so that the block moves in a circular path from B to C.
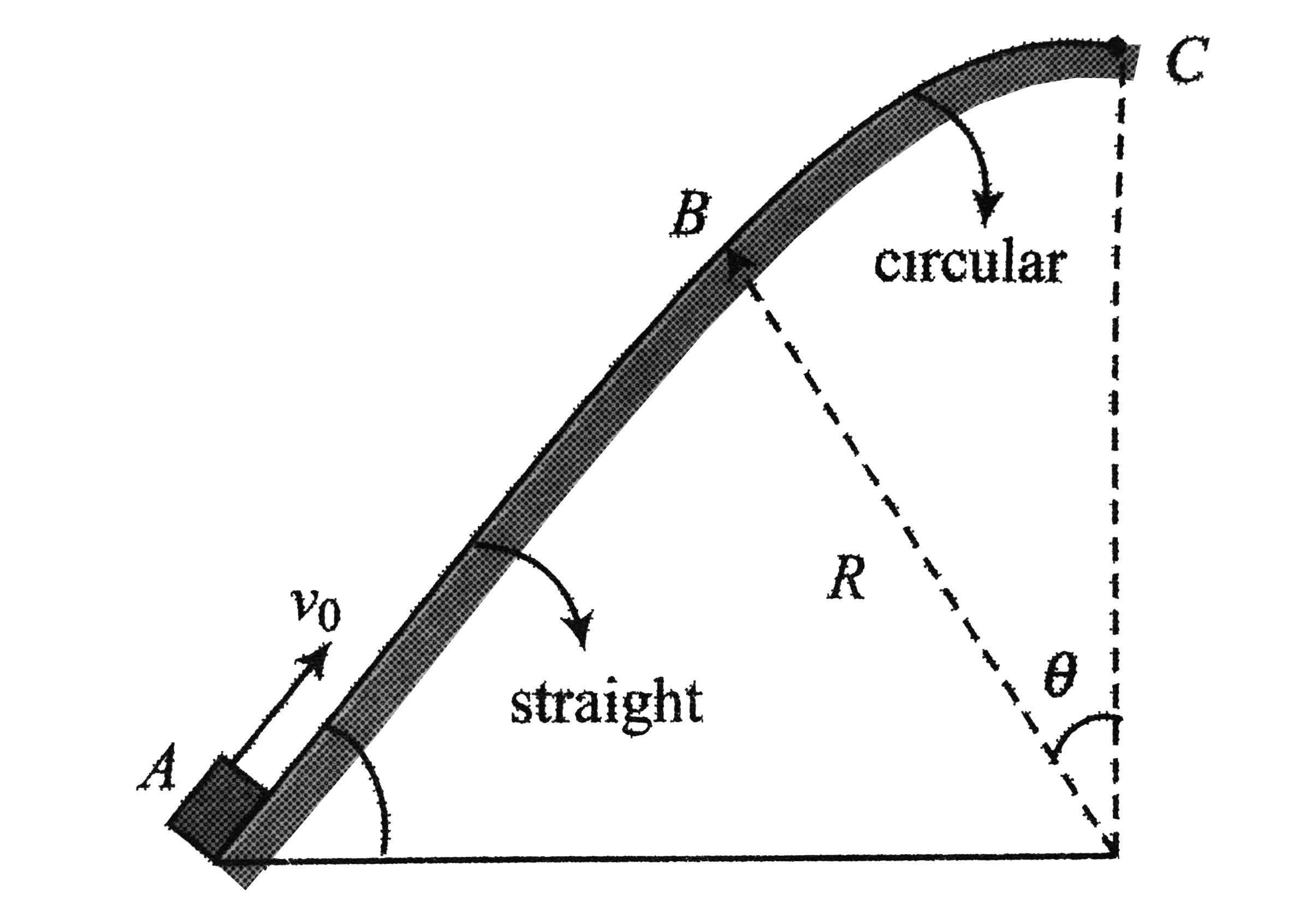 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A person throws a ball in vertical plane such that velocity of ball along horizontal is Vx and along vertical is vγ. Coefficinet of friction between man and gound is μ. Necessary condition so that man always remains at rest will be (Note: the process is done in time Δt0)
AVx>μVyBVx≤μVyCVy≤μVxDNone of these - Question 2 - Select One
A block is resting on a horizontal plate in the xy plane and the coefficient of friction between block and plate is μ. The plate begins to move with velocity v=bt2 in x direction At what time will the block start sliding on the plate?
AμbgBμbg2CμgbDμg2b - Question 3 - Select One
A block B is pushed momentarily along a horizontal surface with an initial velocity v. If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time
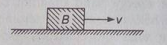 AvgμBgμvCgvDvg
AvgμBgμvCgvDvg
A ball of mass m=1kg falling vertically with a velocity v0=2m/s strikes a wedge of mass M=2kg kept o a smooth, horizontal surface as shown in figure. The coefficient of resitution between the ball and the wege is e=1/2. Find the velocity of the wedge is e=1/2. find the velocity of the wedge and the ball immediately after collison.
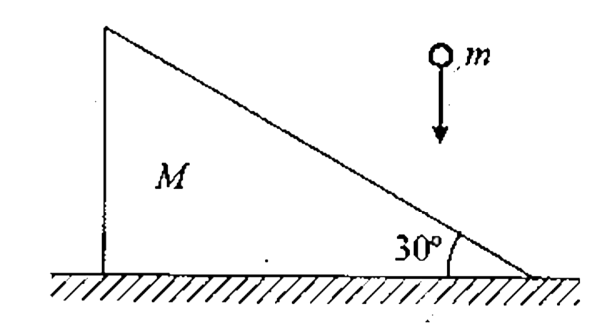 View Solution
View SolutionA man, in a lift ascending with the acceleration fm/sec2, throws a ball vertically upwards with a velocity v and catches it after time t1 . Afterwards when the lift is descending with the same acceleration the man again throws a ball vertically upwards with the same velocity and catches it after time t2 . The velocity v and acceleration f in terms.of t1,t2 where g is the acceleration due to gravity.
View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v. If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time
 View Solution
View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If mu is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:
 View Solution
View SolutionSuppose a ball is projected with speed u at an angle α with horizontal. It collides at some distance with a wall parallel to y-axis.
Let vx and vy be the components of its velocity along x and y-directions at the time of impact with wall. Coefficient of restitution between the ball and the wall is e. Component of its velocity along y-diection (common tangent) vy will remain unchanged while component of its velocity along x -direction (common normal) vx will become evx is opposite direction.
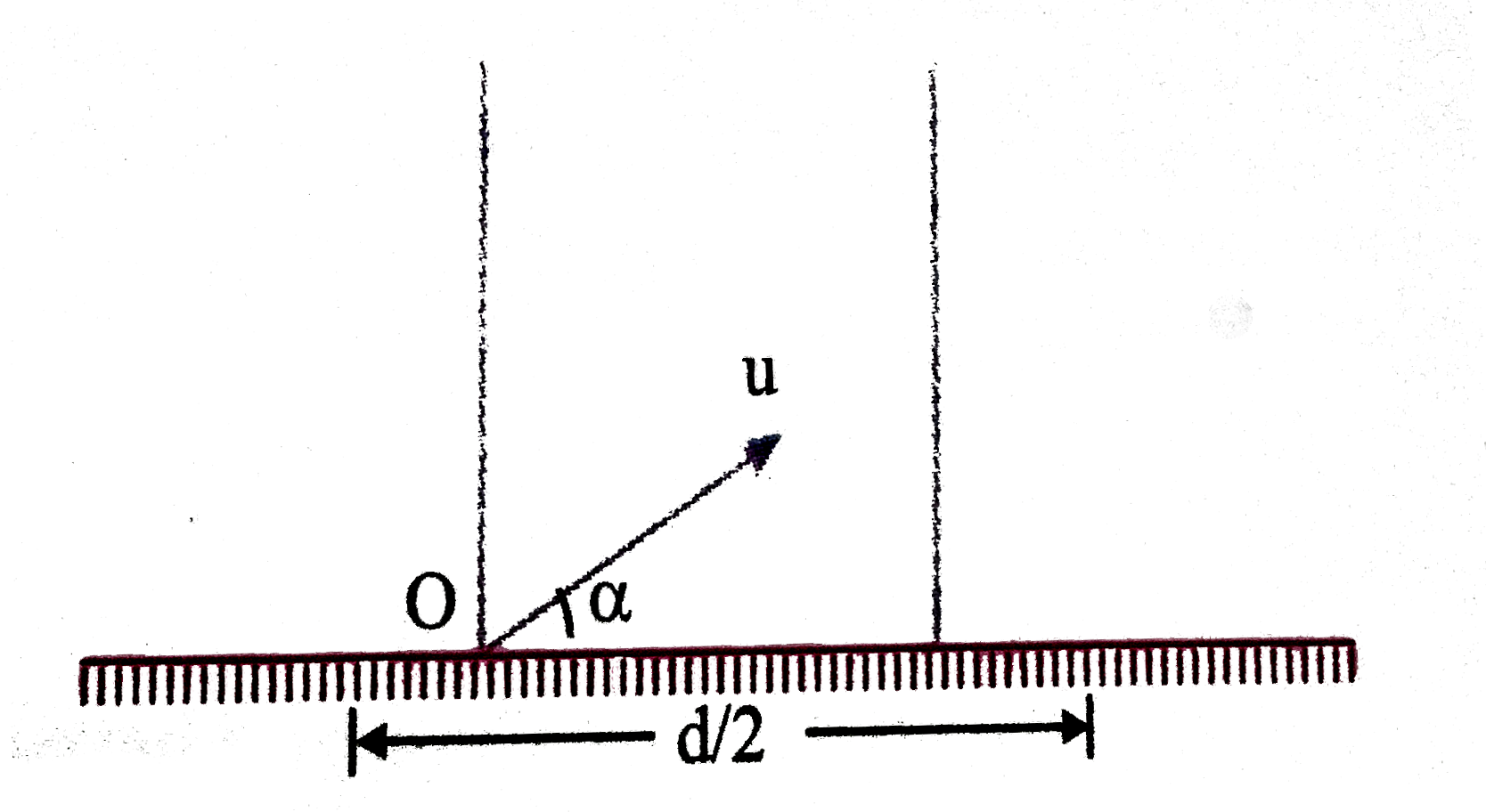
The situation shown in the figure a small ball is projected at an angle α between two vertical walls such that in the absence of the wall its range would have been 5d. Given that all the collisions are perfectly elastic (for first and second problems), the walls are supposed to be very tall.
The total time taken by the ball to come back to the ground (if collision is inelastic) isView Solution

