For each positive integer k, let Sk denote the increasing arithmetic sequence of integers whose firstterm is 1 and whose common difference is k. For example, S3 is the sequence 1,4,7,10.......Find thenumber of values of k for which Sk contain the term 361.
Step by step video & image solution for For each positive integer k, let S_k denote the increasing arithmetic sequence of integers whose firstterm is 1 and whose common difference is k. For example, S_3 is the sequence 1, 4, 7, 10.......Find thenumber of values of k for which S_k contain the term 361. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Let Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1∣∣(k2−3k+1)Sk∣∣ is ____________
View SolutionLet sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
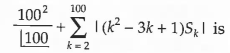 is
is
View SolutionIf the positive integer k denotes an increasing parallel series, the first term of which is 1 and the common denominator. eg S_3 ,1,4,7,10...... The parallel range displayed by is the number of values of k. If S_k In verse 361 comes.
View SolutionFor positive integers k=1,2,3,....n,, let Sk denotes the area of △AOBk such that ∠AOBk=kπ2n, OA=1 and OBk=k The value of the limn→∞1n2n∑k−1Sk is
View SolutionConsider an AP with first term a and the common difference 'd' Let Sk denote the sum of its first k terms. If SkxSx is independent of x then
View SolutionLet Sk be the sum of an infinite G.P. series whose first term is k and common ratio is kk+1(k>0). Then the value of ∞∑k=1(−1)ksk is equal to
View SolutionLet {a1,a2,a3......} be a strictly increasing sequence of positive integers in an arithmetic progression. Prove that there is an infinite subsequence of the given sequence whose terms are in a geometric progression.
View SolutionConsider an A.P. with first term a and common difference d. Let Sk denote the sum of the first k terms. If SkxSx is independent of x, then
View Solution
