If the gravitational force had varied as r−5/2 instead of r−2,the potential energy of a particle at a distance ‘r’ from the centre of the earth would be directly proportional to
r−1
r−2
r−3/2
r−5/2
To solve the problem, we need to determine how the potential energy U of a particle varies with distance r from the center of the Earth when the gravitational force F varies as r−5/2.
1. Understand the relationship between force and potential energy:
The gravitational force F can be expressed in terms of potential energy U as:
F=−dUdr
This means that the force is the negative gradient of the potential energy.
2. Express the gravitational force:
Given that the gravitational force varies as r−5/2, we can write:
F=k⋅r−5/2
where k is a constant.
3. Set up the equation for potential energy:
From the relationship between force and potential energy, we have:
−dUdr=k⋅r−5/2
4. Integrate to find potential energy:
To find U, we integrate the force with respect to r:
dU=−k⋅r−5/2dr
Integrating both sides gives:
U=−k∫r−5/2dr
5. Perform the integration:
The integral of r−5/2 is:
∫r−5/2dr=r−3/2−3/2=−23r−3/2
Therefore, we have:
U=−k(−23r−3/2)+C
Simplifying this gives:
U=2k3r−3/2+C
6. Determine the proportionality:
The potential energy U is directly proportional to r−3/2. Thus, we can conclude:
U∝r−3/2
Conclusion:
The potential energy of a particle at a distance r from the center of the Earth would be directly proportional to r−3/2.
The gravitational force F can be expressed in terms of potential energy U as:
F=−dUdr
This means that the force is the negative gradient of the potential energy.
Given that the gravitational force varies as r−5/2, we can write:
F=k⋅r−5/2
where k is a constant.
From the relationship between force and potential energy, we have:
−dUdr=k⋅r−5/2
To find U, we integrate the force with respect to r:
dU=−k⋅r−5/2dr
Integrating both sides gives:
U=−k∫r−5/2dr
The integral of r−5/2 is:
∫r−5/2dr=r−3/2−3/2=−23r−3/2
Therefore, we have:
U=−k(−23r−3/2)+C
Simplifying this gives:
U=2k3r−3/2+C
The potential energy U is directly proportional to r−3/2. Thus, we can conclude:
U∝r−3/2
The potential energy of a particle at a distance r from the center of the Earth would be directly proportional to r−3/2.
Topper's Solved these Questions
Similar Questions
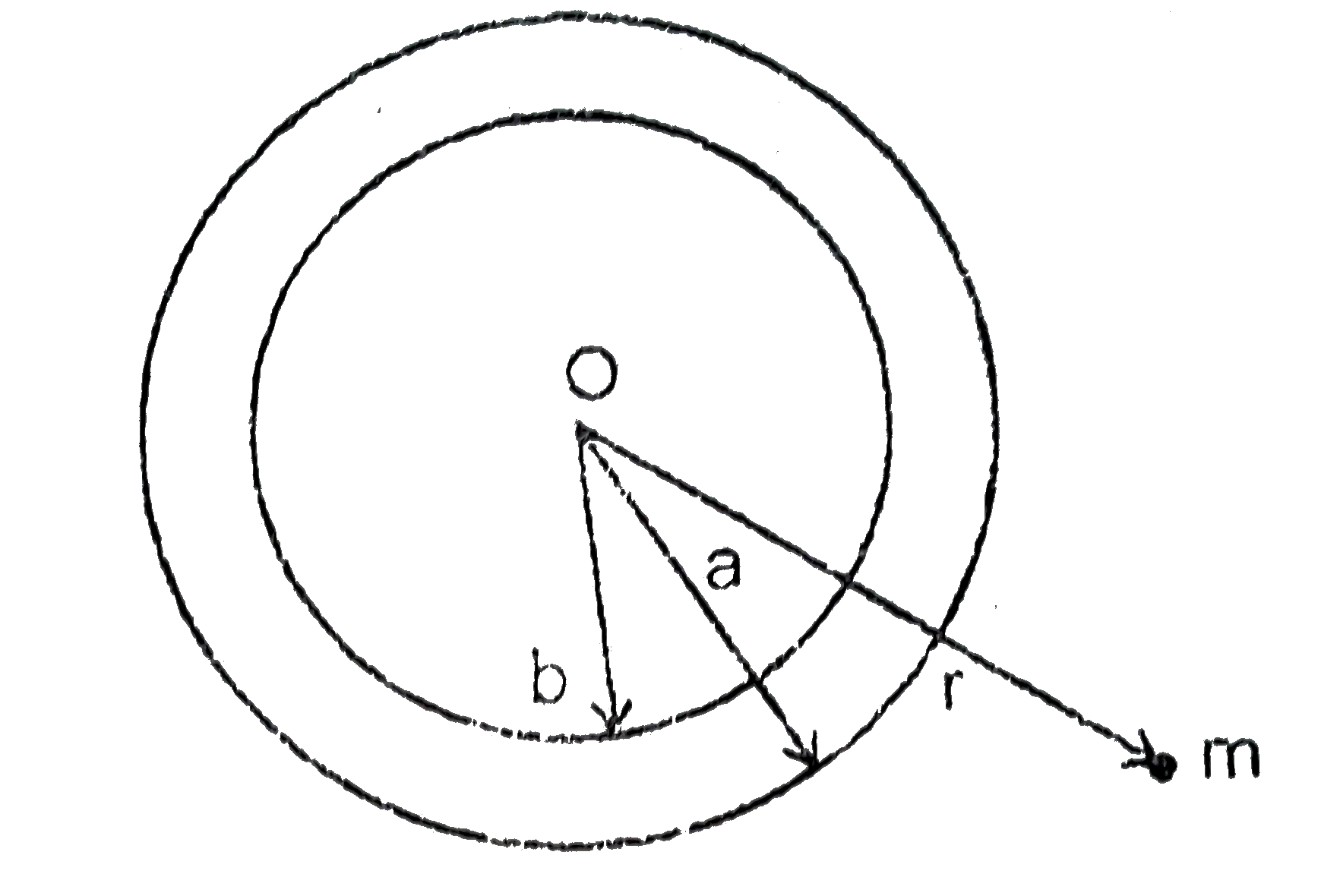
A sphere of density ρ and radius a has a concentric of radius b as shown in the
(a) Sketch the gravitational force exerted by the spehre on the particle of mass m located at a distance r from the centre of the sphere as a function of r in the range 0≤r≤∞
(b) Sketch the corresponding curve for the potential energy u (r) of the system
 ,View Solution
,View SolutionThe potential at a distance R/2 from the centre of a conducting sphere of radius R will be
View Solution
Knowledge Check
- Question 1 - Select One
If the gravitational potential energy of a body at a distance r from the centre of the earth is U, then it's weight at that point is
AUBU2rCU2rDUr - Question 2 - Select One
The gravitational potential energy of a body at a distance r from the center of the earth is U. The force at that point is :
AUr2BUrCUrDUr2 - Question 3 - Select One
The gravitational potential energy of a body at a distance r from the center of the earth is U . The force at that point is
AUr2BUrCUeDUr
The gravitational potential energy of a body at a distance r from the centre of earth is U. Its weight at a distance 2r from the centre of earth is
View SolutionThe gravitational potential energy at a body of mass m at a distance r from the centre of the earth is U. What is the weight of the body at this distance ?
View SolutionThe magnitude of gravitational potential energy of a body at a distance r from the centre of earth is u. Its weight at a distance 2r from the centre of earth is
View SolutionIf R= radius of the earth and g= acceleration due to gravity on the surface of the earth, the acceleration due to gravity at a distance (r>R) from the centre of the earth is proportional to
View SolutionIf R= radius of the earth and g= acceleration due to gravity on the surface of the earth, the acceleration due to gravity at a distance (r<R) from the centre of the earth is proportional to
View Solution

