Seven identical disc are arranged in a hexagonal, planar pattern so as to touch each neighbour, as shown in the figure. Each disc has mass m and radius r. What is the moment of inertia of the system of seven disks about an axis passing through the centre of central disk and normal to plane of all disks ?
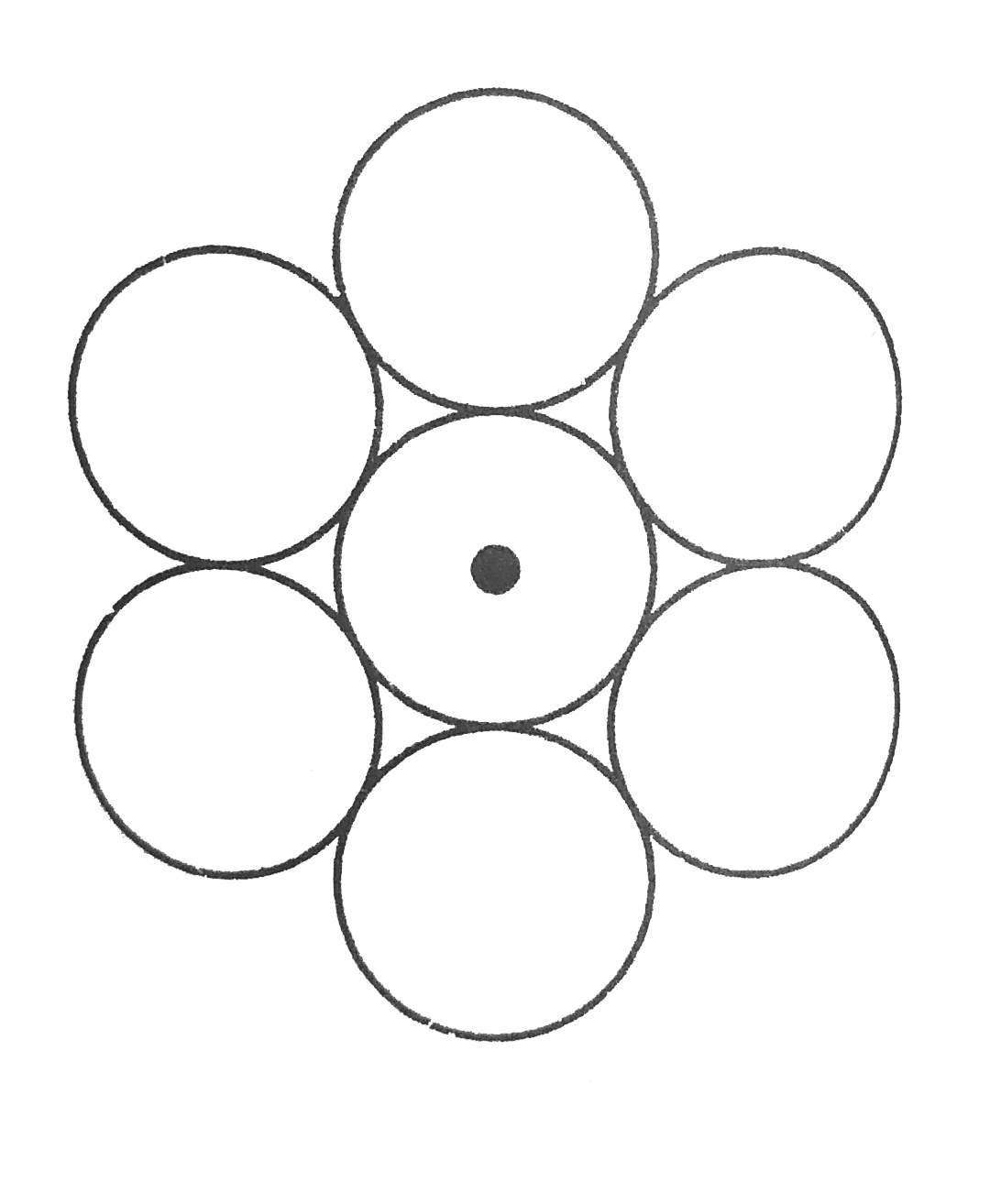 .
.
552mr2
1272mr2
1112mr2
55mr2
Step by step video & image solution for Seven identical disc are arranged in a hexagonal, planar pattern so as to touch each neighbour, as shown in the figure. Each disc has mass m and radius r. What is the moment of inertia of the system of seven disks about an axis passing through the centre of central disk and normal to plane of all disks ? . by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
Calculate the moment of inertia of a disc of radius R and mass M, about an axis passing through its centre and perpendicular to the plane.
View SolutionCalculate the moment of Inertia of a semicircular disc of mass M and radius R about an axis passing through its centre and perpendicular to its plane.
View Solution
Knowledge Check
- Question 1 - Select One
Moment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
A1/2MR2BMR2C1/4MR2D3/4MR2 - Question 2 - Select One
The moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is
AMR2B12MR2C32MR2D72MR2 - Question 3 - Select One
The moment of inertia of a uniform circular disc of radius R and mass M about an axis passing from the edge of the disc and normal to the disc is.
A12MR2BMR2C72MR2D32MR2
A disc has mass 9 m. A hole of radius R/3 is cut from it as shown in the figure. The moment of inertia of remaining part about an axis passing through the centre 'O' of the disc and perpendicular to the plane of the disc is :
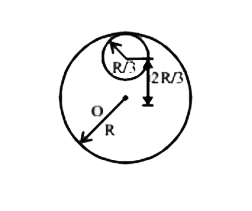 View Solution
View SolutionSeven identical coins are rigidly arranged on a flat table in the pattern shown below so that each coin touches its neighbors. Each coin is a thin disc of mass m and radius r. Note that the moment of inertia of an individual coin about an axis passing through centre and perpendicular to the plane of the coin is m2/2
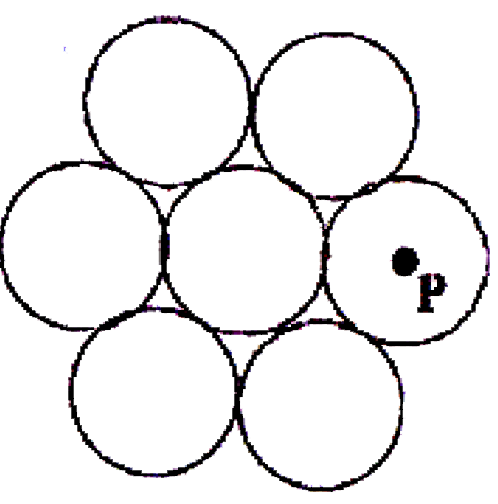
The moment of inertia of the system of seven coins about an axis that passes through the point P (the centre of the coin positioned directly to the right of the central coin) and perpendicular to the plane of the coins is–View SolutionFour particles each of mass m are lying symmetrically on the rim of a disc of mass M and radius R. Moment of inertia of this system about an axis passing through one of the particles and I to plane of disc is
View SolutionThe moment of inertia of a uniform circular disc of mass M and radius R about any of its diameters is 14MR2. What is the moment of inertia of the disc about an axis passing through its centre and normal to the disc?
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View Solution

