Two sources of equal emf are connected to an external resistance R. The internal resistance of the two sources areR1andR2(R1>R1). If the potential difference across the source having internal resistance R2 is zero, then
R=R2−R1
R=R2×(R1+R2)/(R2−R1)
R=R1R2/(R2−R1)
R=R1R2/(R1−R2)
To solve the problem step by step, we will analyze the circuit with two sources of equal EMF connected to an external resistance R. The internal resistances of the two sources are R1 and R2, where R2>R1. We need to find the relationship between the external resistance R and the internal resistances given that the potential difference across the source with internal resistance R2 is zero.
Step 1: Understand the Circuit Configuration
We have two sources of equal EMF E connected in series with an external resistance R. The internal resistances are R1 and R2 respectively.
Step 2: Write the Expression for Current
The total resistance in the circuit is the sum of the external resistance and the internal resistances:
Rtotal=R+R1+R2
The current I flowing through the circuit can be expressed as:
I=2ER+R1+R2
Step 3: Analyze the Condition of Zero Potential Difference
Since the potential difference across the source with internal resistance R2 is zero, we can set up the equation:
E−I⋅R2=0
This implies:
E=I⋅R2
Step 4: Substitute the Expression for Current
Substituting the expression for I into the equation gives:
E=(2ER+R1+R2)⋅R2
Step 5: Simplify the Equation
Rearranging the equation, we have:
E(R+R1+R2)=2ER2
Dividing both sides by E (assuming E≠0):
R+R1+R2=2R2
Step 6: Isolate R
Now, we can isolate R:
R=2R2−R1−R2
This simplifies to:
R=R2−R1
Conclusion
Thus, the relationship between the external resistance R and the internal resistances is:
R=R2−R1
We have two sources of equal EMF E connected in series with an external resistance R. The internal resistances are R1 and R2 respectively.
The total resistance in the circuit is the sum of the external resistance and the internal resistances:
Rtotal=R+R1+R2
The current I flowing through the circuit can be expressed as:
I=2ER+R1+R2
Since the potential difference across the source with internal resistance R2 is zero, we can set up the equation:
E−I⋅R2=0
This implies:
E=I⋅R2
Substituting the expression for I into the equation gives:
E=(2ER+R1+R2)⋅R2
Rearranging the equation, we have:
E(R+R1+R2)=2ER2
Dividing both sides by E (assuming E≠0):
R+R1+R2=2R2
Now, we can isolate R:
R=2R2−R1−R2
This simplifies to:
R=R2−R1
Thus, the relationship between the external resistance R and the internal resistances is:
R=R2−R1
Topper's Solved these Questions
Similar Questions
Two cells of same emf ε, but different internal resistances r1 and r2 are connected to an external resistance R, as shown. The voltmeter V reads zero. Find R in terms of r1 and r2, and the voltage across the cell of internal resistance r2.
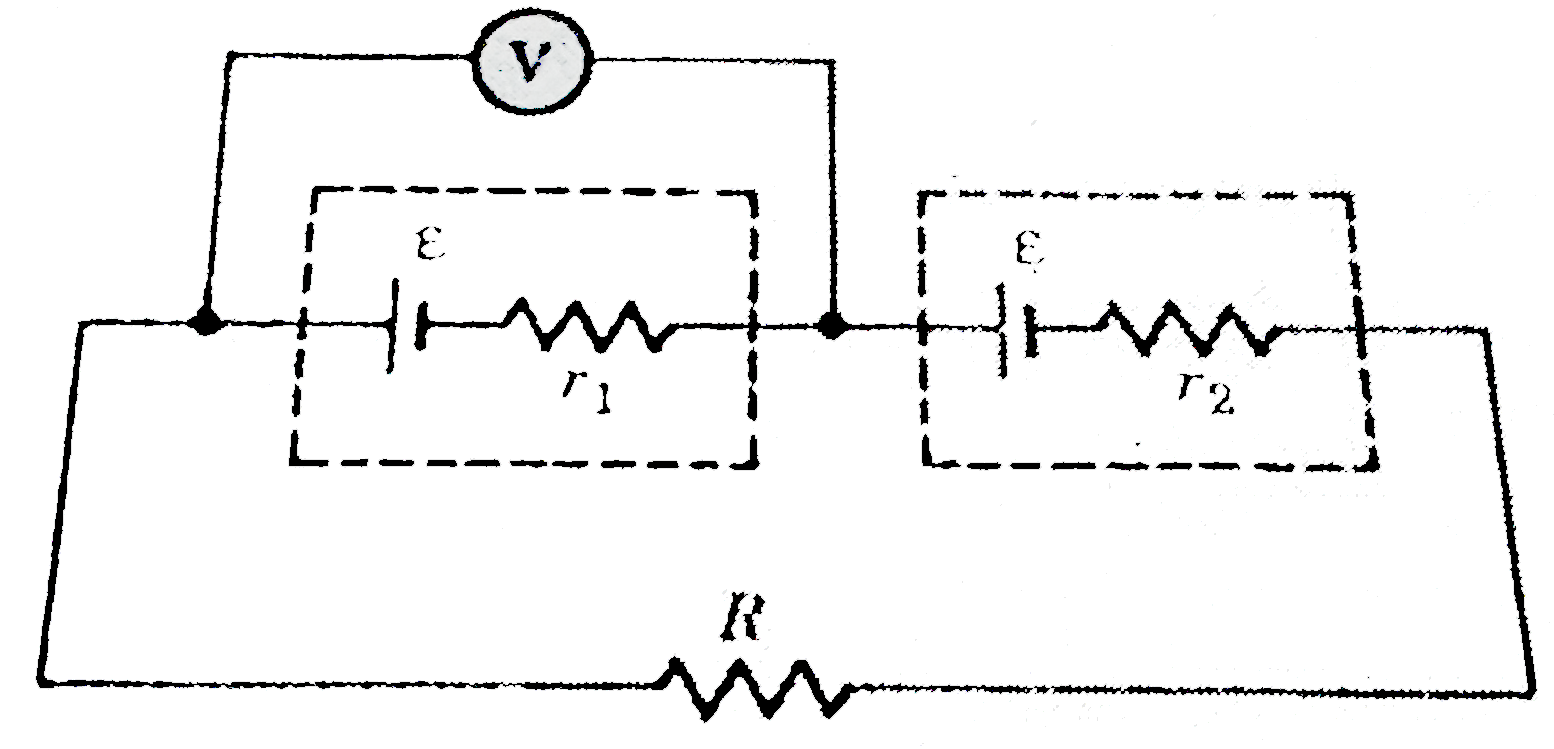
View SolutionTwo sources of current of equal emf are connected in series and having different internal resistance r1 and r2(r2>r1). Find the external resistance R at which the potential difference across the terminals of one of the sources becomes equal to zero.
View Solution
Knowledge Check
Two sources of equal emf are connected to an external resistance R. The internal resistance of the two sources are R1andR2(R1>R1). if the potential difference across the source having internal resistance R2 is zero, then
AR=R2−R1BR=R2×(R1+R2)/(R2−R1)CR=R1R2/(R2−R1)DR=R1R2/(R1−R2)Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
AR1−R2BR1+R22CR1−R22DR1+R2Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
Ar1+r2Br1−r2Cr1+r22Dr1−r22
Two cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potentail difference across the first cell is zero the value of R is
View SolutionTwo cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potential difference across the first cell is zero.
View SolutionTwo cells, having the same emf, are connected in series through an external resistance R. Cells have internal resistance r1 and r2(r1>r2) respectively. When the circuit is closed, the potential difference across the first cell is zero.
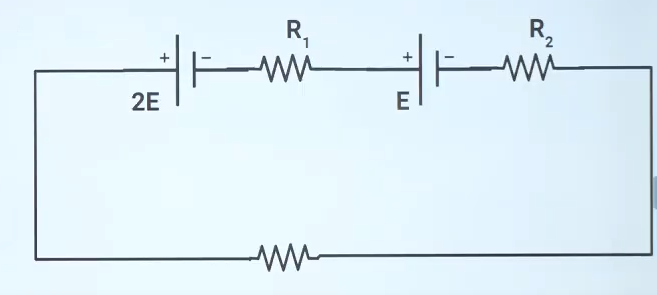
View SolutionInternal resistance of battery of emf 2E is R1 and battery of emf E is R2. If the potential difference across the cell of emf 2E is zero, then value of R is
View SolutionIf E is the emf of a cell of internal resistance r and external resistance R, then potential difference across R is given as
View Solution
