A metal rod of length l cuts across a uniform magnetic field B with a velocity v. If the resistance of the circuit of which the rod forms a part is r, then the force required to move the rod is
B2l2vr
Blvr
B2lvr
B2l2v2r
To find the force required to move a metal rod of length l across a uniform magnetic field B with a velocity v, we can follow these steps:
Step 1: Determine the Induced EMF
When the rod moves through the magnetic field, it cuts the magnetic field lines, which induces an electromotive force (EMF) in the rod. The induced EMF (E) can be calculated using the formula:
E=B⋅l⋅v
where:
- B is the magnetic field strength,
- l is the length of the rod,
- v is the velocity of the rod.
Step 2: Calculate the Induced Current
The induced EMF causes a current to flow in the circuit. According to Ohm's law, the current (I) can be calculated as:
I=Er
Substituting the expression for induced EMF:
I=B⋅l⋅vr
Step 3: Calculate the Magnetic Force on the Rod
The magnetic force (FB) acting on the current-carrying rod can be calculated using the formula:
FB=B⋅I⋅l
Substituting the expression for current:
FB=B⋅(B⋅l⋅vr)⋅l
This simplifies to:
FB=B2⋅l2⋅vr
Step 4: Determine the Required Force to Move the Rod
To keep the rod moving with a constant velocity v, we need to apply a force (F) equal in magnitude but opposite in direction to the magnetic force. Therefore, the required force is:
F=FB=B2⋅l2⋅vr
Final Answer
The force required to move the rod is:
F=B2⋅l2⋅vr
---
When the rod moves through the magnetic field, it cuts the magnetic field lines, which induces an electromotive force (EMF) in the rod. The induced EMF (E) can be calculated using the formula:
E=B⋅l⋅v
where:
- B is the magnetic field strength,
- l is the length of the rod,
- v is the velocity of the rod.
The induced EMF causes a current to flow in the circuit. According to Ohm's law, the current (I) can be calculated as:
I=Er
Substituting the expression for induced EMF:
I=B⋅l⋅vr
The magnetic force (FB) acting on the current-carrying rod can be calculated using the formula:
FB=B⋅I⋅l
Substituting the expression for current:
FB=B⋅(B⋅l⋅vr)⋅l
This simplifies to:
FB=B2⋅l2⋅vr
To keep the rod moving with a constant velocity v, we need to apply a force (F) equal in magnitude but opposite in direction to the magnetic force. Therefore, the required force is:
F=FB=B2⋅l2⋅vr
The force required to move the rod is:
F=B2⋅l2⋅vr
Topper's Solved these Questions
Similar Questions
A glass rod of length l moves with velocity in a uniform magnetic field B. What is the e.m.f. induced in the rod ?
View SolutionAs shown in figure, a metal rod completes the circuit. The circuit area is perpendicular to a magnetic field with B=0.15T. If the resistance of the total circuit is 3Ω, how large a force is needed to move the rod as indicated with a constant speed of 2 m/s?
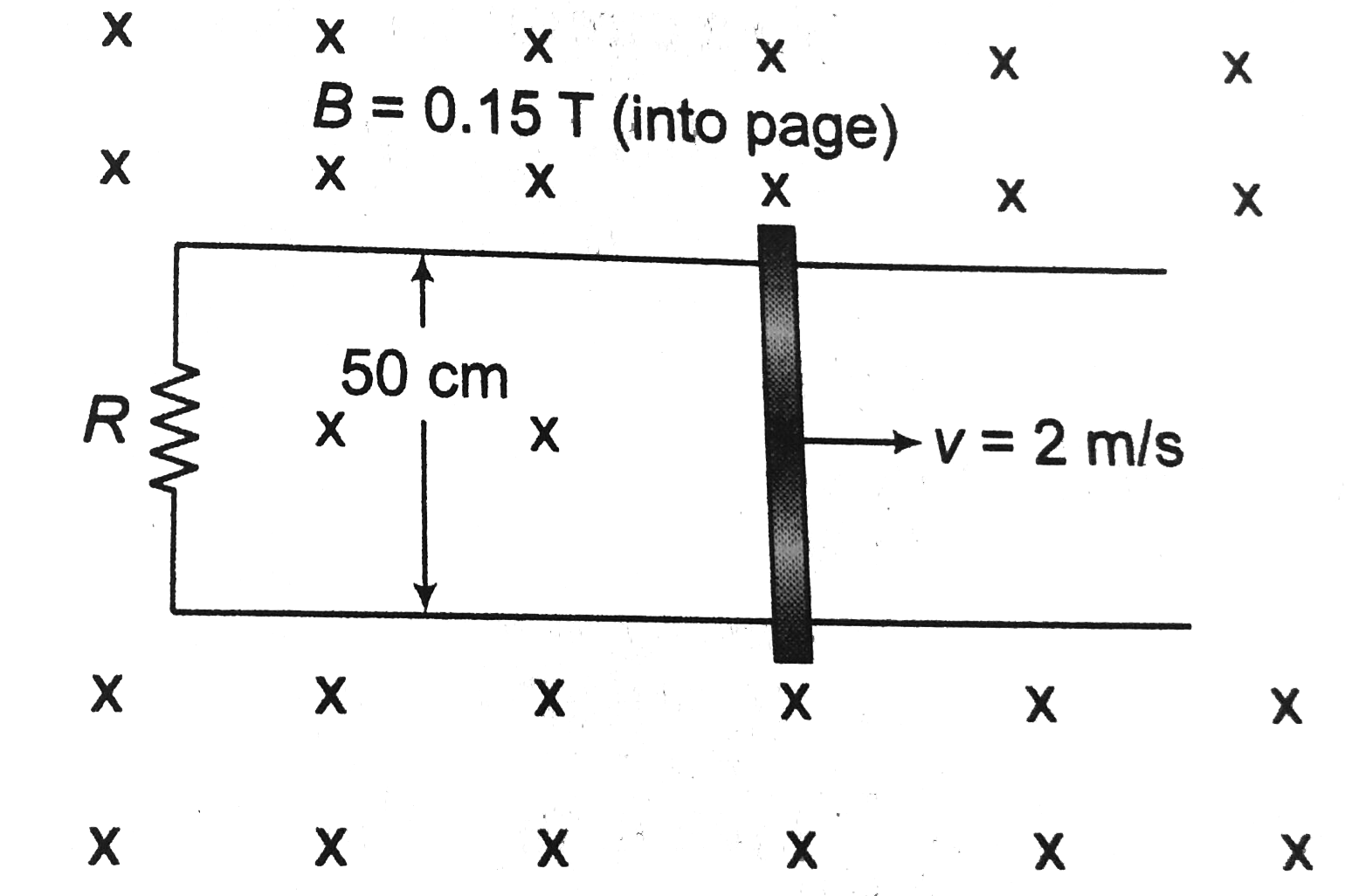 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A metallic rod completes its circuit as shown in the figure. The circuit is normal to a magnetic field of B=0.15 tesla. If the resistances of the rod is 3Ω the force required to move the rod with a constant velocity of 2m/sec is-
 A3.75×10−3NB3.75×10−2NC3.75×102ND3.75×10−4N
A3.75×10−3NB3.75×10−2NC3.75×102ND3.75×10−4N - Question 2 - Select One
A conducting rod of length l is moving in a transverse magnetic field of strength B with veocity v. The resistance of the rod is R. The current in the rod is
ABlvRBBlvCzeroDB2v2l2R - Question 3 - Select One
A metallic rod completes its circuit as shown in the figure. The circuit is normal to a magnetic field of B=0.15 tesla. If the resistances of the rod is 3Ω the force required to move the rod with a constant velocity of 2m/sec is-
 A3.75×10−3NB3.75×10−2NC3.75×102ND3.75×10−4N
A3.75×10−3NB3.75×10−2NC3.75×102ND3.75×10−4N
" A metal rod of area of cross section A has length L and coefficient of thermal conductivity K The thermal resistance of the rod is "
View SolutionA conducting wire of length l is placed on a rough horizontal surface, where a uniform horizontal magnetic field B perpendicular to the length of the wire exists. Least values of the forces required to move the rod when a current I is established in the rod are observed to be F1 and F2(<F1) for the two possible directions of the current through the rod, respectively. Find the weight of the rod and the coefficient of friction between the rod and the surface.
View SolutionA metallic rod of length L rotates at an angular speed ω, normal to a uniform magnetic field. If the resitance of rod is R the heat dissipated is:
View SolutionA metal rod of length I is moved with velocity v in a uniform magnetic field →B. Emf is induced between the two ends of rod
View SolutionA metal rod of area of cross section A has length L and coefficient of thermal conductivity K the thermal resistance of the rod is .
View Solution

