In the given figure, O is the centre of the circle. If BD=DC and ∠DBC=30∘, find the measure of ∠BAC and ∠BOC.
Video Solution
Text Solution
As BD=DC,
∴∠DCB=∠DBC=30∘
∴∠BDC=180∘−∠DCB−∠DBC=120∘
Now, ABDC is a cyclic quadrilateral.
∴∠BDC+∠BAC=180∘
⇒∠BAC=180∘−120∘=60∘
We know, angle subteded at the center by a chord is double than that of angle subtended at any point on the circle.
∠BOC=2∠BAC=2∗60∘=120∘
|
Updated on:21/07/2023
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, O is the centre of the circle. Then ∠AED measure
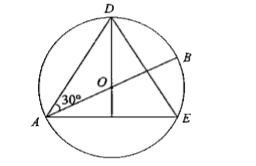 A30∘B45∘C60∘D90∘
A30∘B45∘C60∘D90∘ - Question 2 - Select One
In the given figure, O is the centre of the circle. The measure of ∠ ADB is
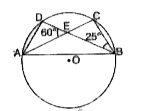 A90∘B85∘C95∘D120∘
A90∘B85∘C95∘D120∘ - Question 3 - Select One
In the given figure O is the centre of the circle and ∠BAC=25∘, then the value of ∠ADB is :
 A40∘B55∘C50∘D65∘
A40∘B55∘C50∘D65∘
In the adjoining figure, O is the centre of the circle.If ∠BAC=40∘, then find the value of ∠ADC.
 View Solution
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=150∘ and ∠BOC=100∘, then find the value of ∠ABC.
 View Solution
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=150∘ and ∠BOC=100∘, then find the value of ∠ABC.
 View Solution
View Solution(i) In the adjoining figure, O is the centre of the circle. If ∠OBC=35∘, then find the value of ∠BAC.

(ii) In the adjoining figure, O is the centre of the circle. If ∠OBC=40∘, then find the value of ∠BAC.
 View Solution
View SolutionIn the given figure, O is the centre of circle. ∠AOC=120∘. Find ∠BAC :
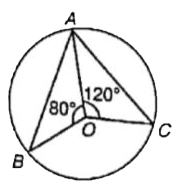 View Solution
View Solution

